Enunciado
Álgebra Linear e Geometria Analítica - Álgebra Linear - 3ª Edição - J. L. Boldrini- Ed: 3º - Capítulo 11.7.2 - Ex. 1a
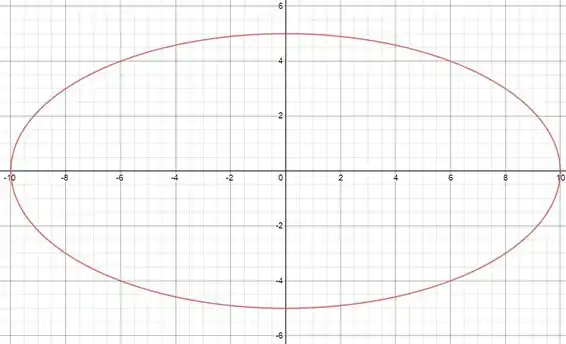
Esboce o gráfico das cônicas a seguir, determinando seus focos, diretrizes e excentricidade.
Passo 1
Como ambos os termos quadráticos são positivos, sabemos que temos uma elipse! Dividindo todos por e deixando na forma padrão:
Passo 2
Temos uma elipse com seu eixo maior no eixo de a e seu eixo menor em de a :
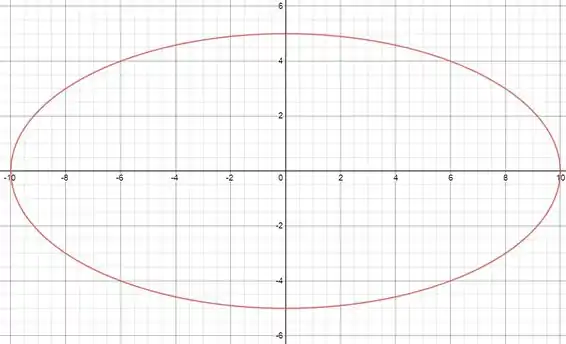
Passo 3
Pela definição, seus focos serão e . é definido como:
Ou seja:
E sua excentricidade:
Suas diretrizes serão:
Resposta
Exercícios de Livros Relacionados
5.1.3. Escreva as equações das seguintes hipérboles: (b) Os focos são F1 = (−1, −1) e F2 = (1, 1) e satisfaz | distância (P, F1) – distância (P, F2)| = 2;
5.1.5 Determinar a equação e identificar a trajetória de um ponto que se move de maneira que sua distância ao ponto F = (6, 0) é sempre igual a duas vezes sua distância a reta 2x − 3 = 0
5.1.3. Escreva as equações das seguintes hipérboles: (a) Os focos são F1 = (3, −1) e F2 = (3, 4) e satisfaz | distância (P, F1) – distância (P, F2) | = 3;
Para todo ponto P =(m,n) na hipérbole H : x 2 a 2 - y 2 b 2 = 1 , mostre que a reta r :m x a 2 - n y b 2 = 1 tem apenas um ponto P em comum com H. A reta r chama-se a tangente de H no ponto P
Quais são as coordenadas dos focos da hipérbole x 2 9 - y 2 4 = 1