Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Álgebra Linear e Geometria Analítica - Álgebra Linear - 3ª Edição - J. L. Boldrini- Ed: 3º - Capítulo 11.7.2 - Ex. 1b

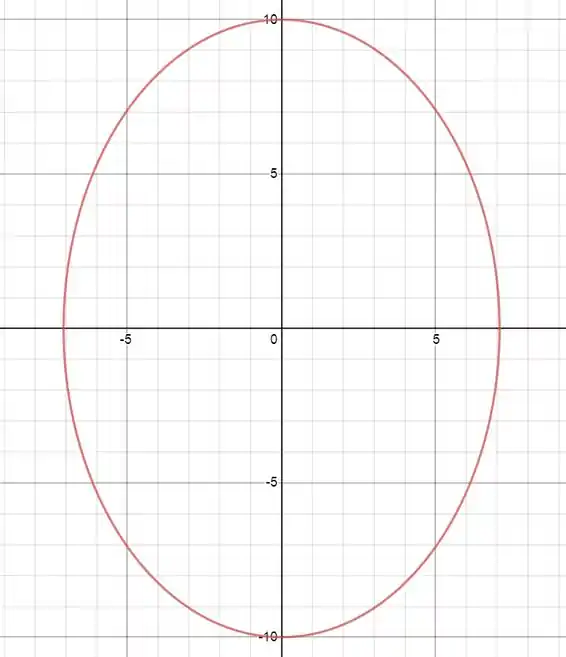
Esboce o gráfico das cônicas a seguir, determinando seus focos, diretrizes e excentricidade.

2 x 2 + y 2 = 100

Passo 1

Dividindo todo mundo por 100 para ficarmos com a forma canônica:

x 2 5 2 2 + y 2 10 2 = 1

Temos uma elipse com eixo maior no eixo y ! Com a = 10 e b = 5 2 .

Passo 2

Fazendo um esboço, temos:

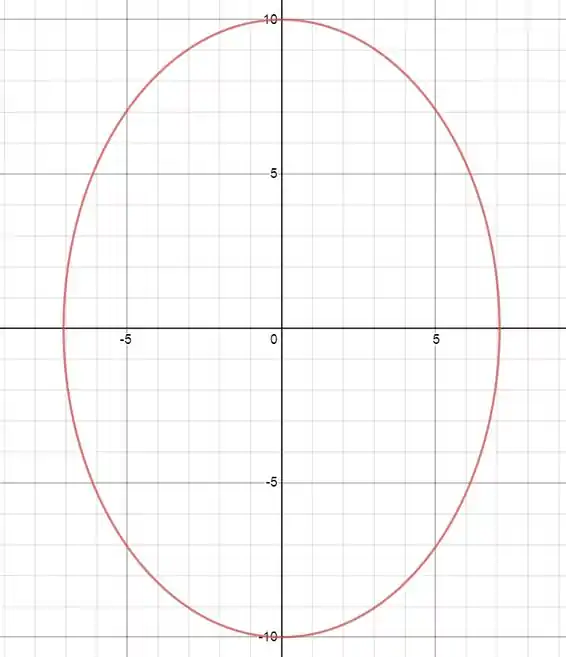
Passo 3

Seus focos estão em F 1 = ( 0 ,   - c ) e F 2 = 0 ,   c . Onde:

c = a 2 - b 2 = 100 - 50 = 5 2

Sua excentricidade:

e = c a = 5 2 10 = 2 2

Suas retas diretrizes serão dadas por:

y = - a e ; y = a e

→ y = ± 10 2 2 = ± 20 2

Resposta

F 1 = 0 ,   - 5 2 ; F 2 = 0 ,   5 2

y = ± 20 2

e = 2 2

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Quais são as coordenadas dos focos da hipérbole x y=1 ?
Prove que a tangente á hipérbole x y=1 no ponto P=( 5 ,1 / 5 ) é a bissetriz do ângulo F P ^ F , onde FeF ′ são os focos.
Dados A, C e F, números positivos, considere as equações ±A x ²±C y ²=±F ² ² . Escolhendo os sinais + e − das oito maneiras poss´ıveis, mostre que em cada caso se obtém uma elipse, uma hipérbole ou o
Dado arbitrariamente R0, ache um ponto x , y na hipérbole x 2 a 2 - y 2 b 2 = 1 tal que x 2 + y 2R . Conclua que toda hipérbole é um conjunto ilimitado, isto é, não pode estar contida num disco de cen
Cada uma das equações a seguir representa o conjunto vazio, um ponto, uma reta, um par de retas paralelas ou um par de retas que se cortam na origem. Decida cada situação e determine as retas, se for