Enunciado
Álgebra Linear e Geometria Analítica - Álgebra Linear - 3ª Edição - J. L. Boldrini- Ed: 3º - Capítulo 11.7.2 - Ex. 1l
Esboce o gráfico das cônicas a seguir, determinando seus focos, diretrizes e excentricidade.
Passo 1
Temos uma variável quadrática e outra variável linear, isso quer dizer que temos uma parábola! A variável linear define o eixo o qual a parábola está crescendo, nesse caso, o eixo . Na forma canônica:
Temos que . Como a parábola está crescendo na direção positiva do eixo .
Passo 2
O gráfico da cônica fica assim:
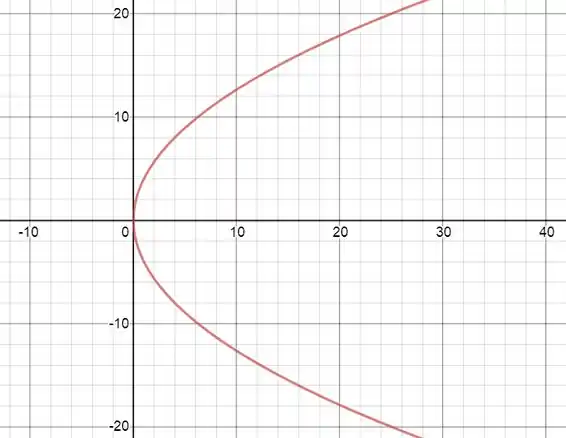
Passo 3
Seu foco será
Sua excentricidade , para qualquer parábola.
E a reta diretriz será a reta
Resposta
Exercícios de Livros Relacionados
Cada uma das equações a seguir representa o conjunto vazio, um ponto, uma reta, um par de retas paralelas, uma cônica ou um par de retas que se cortam na origem. Decida cada situações e determine as r
O eixo de uma hipérbole mede 6 e seus focos, situados sobre o eixo OY, são F'=( 0 ,- 4 )eF=( 0 ,4 ) . Qual é a equação dessa hipérbole?
Dados um ponto F, uma reta ∆ que não contém F e um número positivo e, seja X o conjunto dos pontos P do plano tais que d P , F d ( P , ∆ ) = e Prove:a) Se e1 então X é uma hipérbole.
Mostre que x =a cos t , y =sin t cos t equações paramétricas de uma hipérbole. Qual é o domínio da variável t e quais são os focos dessa hipérbole?
Lembrando que m 2 -n 2 =m+n m–n , mostre que x–x 2 - a 2 = a 2 x +x 2 - a 2 e use este fato para concluir que, atribuindo a x valores muito grandes em módulo, o ponto ( x , b a x ) na assíntota da hip