Enunciado
Álgebra Linear e Geometria Analítica - LIMA, Elon L. Geometría analítica e Álgebra Linear- Ed: 2º - Capítulo 8.Problemas - Ex. 3
Escreva, sob a forma , a equação da reta que passa pela origem e faz um ângulo de com a reta .
Passo 1
Faaala, galeeeera!
Primeiramente, vamos obter o valor de a, ou seja, do coeficiente angular da equação. Para isso, temos:
Isolando y:
O coeficiente angular dessa equação é . Com essa informação podemos calcular o coeficiente angular da equação que queremos determinar.
Isolando , temos:
Como , já temos uma parte da equação. Agora precisamos obter e .
Temos que:
Como a reta passa pela origem, temos, substituindo o ponto :
Logo, nossa equação será somente:
Abaixo temos a representação do problema:
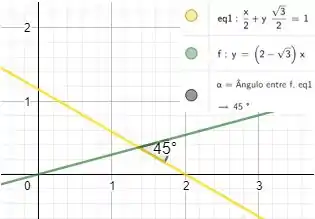
Prontinho!
Resposta
Exercícios de Livros Relacionados
Determinar o valor de n para que seja de 30 ° o ângulo entre as retasa) r 1 : x - 2 4 = y 5 = z 3 e r 2 : y = n x + 5 z = 2 x - 2 b) r 1 : y = n x - 1 z = 2 x e r 2 : eixoO y
Determinar o ângulo entre as seguintes retas:a) r 1 : x = - 2 - t y = t z = 3 - 2 t e r 2 : x 2 = y + 6 1 = z - 1 1 b) r 1 : y = - 2 x + 3 z = x - 2 e r 2 : y = z + 1 - 1 ; x = 4 c) r 1 : x = 1 + 2 t
Determinar o valor de n para que seja de 30 ° o ângulo entre as retasa) r 1 : x - 2 4 = y 5 = z 3 e r 2 : y = n x + 5 z = 2 x - 2 b) r 1 : y = n x - 1 z = 2 x e r 2 : e i x oO y
21. Determinar o ângulo entre as seguintes retas:a) r 1 : x = - 2 - t y = t z = 3 - 2 t e r 2 : x 2 = y + 6 1 = z - 1 1
Disputando uma partida de sinuca com seus amigos, Paulinho viu-se diante da situação ilustrada na Figura 19-3 (a), em que o ponto B representa a bola branca, P ,a preta, e R a rosa (esta era a bola da