Se, no triângulo , as medianas que partem dos vértices e são iguais, prove que os lados e são iguais, logo o triângulo é isósceles. [Escolha um sistema de eixos no qual .]
Passo 1
E aí, galera! Beleza?
Observe o triângulo qualquer abaixo. Temos o seguimento que parte de e vai até o ponto , note que essa bissetriz divide o triângulo em dois lados iguais o e . O lado MC é um lado em comum entre os dois triângulos. Logo temos uma relação (lado, ângulo, lado) de congruência de triângulos, em que ambos os lados possuem mesmo tamanho em lados e ângulos. Agora observe as medianas (em rosa) que partem de e . Temos que se os lados e são iguais, já que a mediana divide o seguimento em dois lados iguais.
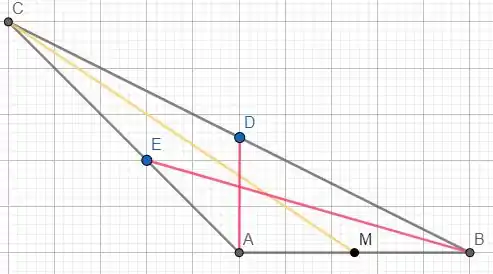
Até a próxima!

Resposta
Observe o triângulo qualquer abaixo. Temos o seguimento que parte de e vai até o ponto , note que essa bissetriz divide o triângulo em dois lados iguais o e . O lado MC é um lado em comum entre os dois triângulos. Logo temos uma relação (lado, ângulo, lado) de congruência de triângulos, em que ambos os lados possuem mesmo tamanho em lados e ângulos. Agora observe as medianas (em rosa) que partem de e . Temos que se os lados e são iguais, já que a mediana divide o seguimento em dois lados iguais.