Enunciado
Álgebra Linear e Geometria Analítica - Anton - Álgebra Linear- Ed: 10º - Capítulo 2.1 - Ex. 17
Nos exercícios 15-18, encontre todos os valores de com os quais (A) = 0
17.
Passo 1
Para calcular o determinante dessa matriz vamos usar a técnica de setas
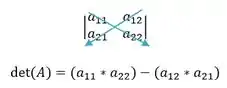
Logo:
Passo 2
Agora que encontramos a função que define o determinante e também sabemos que de acordo com a questão o valor do determinante é . Podemos encontrar o valor de , resolvendo a equação do segundo grau.
Resposta
ou
Exercícios de Livros Relacionados
Nos exercícios 13-19, decida se a matriz é simetrica.19. 0 0 1 0 2 0 3 0 6
Nos exercícios 20-27, calcule o determinante, sabendo que a b c d e f g h i = - 6
Nos exercícios 20-27, calcule o determinante, sabendo que a b c d e f g h i = - 6
Nos Exercícios 5-8, calcule o determinante da matriz. Se a matriz for invertível, use a Equação (2) pra encontrar a inversa.6. 4 1 8 2
Nos Exercícios 5-8, calcule o determinante da matriz. Se a matriz for invertível, use a Equação (2) pra encontrar a inversa.5.3 5 - 2 4