Nos exercícios 9-14, use a técnica de setas para calcular o determinante da matriz.
10.
Passo 1
Para calcular o determinante dessa matriz vamos usar a técnica de setas pedida na questão.

Logo:
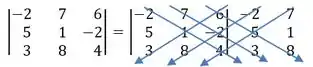
Nos exercícios 9-14, use a técnica de setas para calcular o determinante da matriz.
10.
Para calcular o determinante dessa matriz vamos usar a técnica de setas pedida na questão.

Logo:
