Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Álgebra Linear e Geometria Analítica - Paulo Boulos - Geometria Analítica - Ed: 3º - Capítulo 9.Exercício - Ex. 37

A Figura 9-5 (b), as arestas A B , A C e A D do tetraedro A B C D medem, respectivamente, 2 , 3 e 4 ; os ângulos B Â C , C Â D e D Â B mede, respectivamente, 90 ° , 60 ° e 60 ° ; M é ponto médio de B C , e N é ponto médio de C D . Calcule o cosseno do ângulo M Â N .

Passo 1

Vamos considerar primeiro a figura:

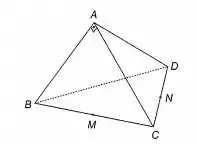
Vamos adotar a base u → ,   v → ,   w → para resolver o problema, com u → = A B → , v → = A C → e w → = A D → . Sabemos que

u → = 2 ,               v → = 3                 e               w → = 4

Além disso,

a n g   u → ,   v → = 90 ° ,                 a n g   u → ,   w → = 60 °                   e                 a n g   v → ,   w → = 60 °

Portanto:

u → ⋅ u → = 2 2 = 4 ,                 v → ⋅ v → = 3 2 = 9                   e               w → ⋅ w → = 4 2 = 16

u → ⋅ v → = 2 ⋅ 3 ⋅ cos ⁡ 90 ° = 0

u → ⋅ w → = 2 ⋅ 4 ⋅ cos ⁡ 60 ° = 4

v → ⋅ w → = 3 ⋅ 4 ⋅ cos ⁡ 60 ° = 6

Passo 2

O passo inicial é escrever os vetores   A M → e   A N → nessa base:

A M → = A B → + B M → = A B → + 1 2   B C → = A B → + 1 2   B A → + A C → = A B → + 1 2 A C → - A B → = 1 2   A B → + 1 2   A C →

A N → = A D → + D N → = A D → + 1 2   D C → = A D → + 1 2   D A → + A C → = A D → + 1 2 A C → - A D → = 1 2   A D → + 1 2   A C →

Escrevendo em termos da base:

A M → = 1 2 u → + 1 2 v →                 e             A N → = 1 2 v → + 1 2 w →

Assim,

A M → 2 = 1 4   u → + v → ⋅ u → + v → = 1 4   u → ⋅ u → + v → ⋅ v → + 2   u → ⋅ v → = 1 4   4 + 9 + 2 ⋅ 0 = 13 4

A N → 2 = 1 4   w → + v → ⋅ w → + v → = 1 4   w → ⋅ w → + v → ⋅ v → + 2   v → ⋅ w → = 1 4   16 + 9 + 2 ⋅ 6 = 37 4

Portanto,

A M → = 13 2                     e                       A N → = 37 2

Passo 3

Para achar o ângulo θ = M Â N , fazemos

cos ⁡ θ = A M → ⋅ A N → A M →   A N →

O produto escalar é

A M → ⋅ A N → = 1 4   u → + v → ⋅ w → + v → = 1 4 ( u → ⋅ w → + u → ⋅ v → + v → ⋅ w → + v → ⋅ v → )

Assim,

A M → ⋅ A N → = 1 4 4 + 0 + 6 + 9 = 19 4

Portanto,

cos ⁡ θ = 19 / 4 13 ⋅ 37 / 4 = 19 481

Portanto,

θ = arccos ⁡ 19 481

Resposta

θ = arccos ⁡ 19 481

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

A Figura 9-5 (a) mostra um paralelepípedo retângulo. Sendo α e β as medidas dos ângulos indicados e γ a medida de A B ^ C , mostre que cos ⁡ γ = s e nαs e nβ
Sejam A , B e C pontos não-colineares, u → = A B → , v → = A C → . Prove que, se a → e u → são de mesmo sentido e o mesmo ocorre com b → e v → , e se a → = b → , então a → + b → é paralelo à bissetriz
Em relação a uma base ortonormal, sabe-se que A B → = 2 ,3 ,1 e A C → = ( - 1 ,3 ,1 ) .a) Verifique que A , B e C são vértices de um triângulo.b) Calcule o comprimento da altura relativa ao vértice A
Sendo e → 1 = ( 1 ,2 ,2 ) , e → 2 = ( 1 ,0 ,1 ) e e → 3 = ( 1 ,1 ,1 ) , aplique o Processo de Ortonormalização de Gram-Schmidt para obter uma base ortonormal a partir da base e → 1 ,e → 2 ,e → 3 .
Na Figura 9-4 (c), a aresta do cubo mede 3 e P é um ponto sobre H F tal que a medida angular entre D P → e D H → é 30 ° . Calcule as normas de D P → e H P → e a medida em radianos do ângulo P D ^ C .