Enunciado
Álgebra Linear e Geometria Analítica - Paulo Boulos - Geometria Analítica - Ed: 3º - Capítulo 10.Exercício - Ex. 10
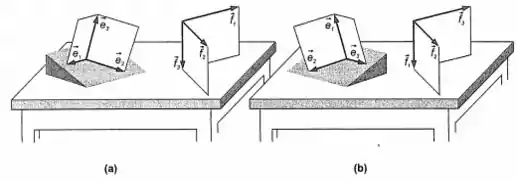
Verifique se as bases e são concordantes ou discordantes nos casos (a) e (b) da Figura 10-4.
Passo 1
O problema quer que verifiquemos se as bases e são concordantes ou discordantes:
Para que elas sejam concordantes, ambas as bases devem ter a mesma orientação.
Passo 2
No item (a), a base é dextra pois satisfaz a regra da mão direita. Da mesma forma, a base também é dextra. Assim, como as duas bases tem a mesma orientação, elas são concordantes.
Já no item (b), a base é dextra, enquanto a base é sinistra, pois satisfaz a regra da mão esquerda. Como elas tem orientações contrárias, elas são discordantes.
Resposta
Concordantes (a) e discordantes (b).
Exercícios de Livros Relacionados
Suponha que { u 1 ,… ,u r ,v 1 ,… ,v s } é um subconjunto L.I de um espaço V . Mostrar que u 1 ,… ,u r ⋂ v 1 ,… ,v s = 0
Se { u 1 ,… ,u i ,… ,u j ,… ,u n } é L.I, mostrar que u 1 ,… ,u i ,… ,u j + α u i ,… ,u n Também é L.I, para todo escalar α .
Suponha que { v 1 ,… ,v n } é um subconjunto L.I de um espaço vetorial. Mostrar que { a 1 v 1 ,… ,a n v n } também é L.I, desde que os escalares a i sejam todos não nulos.
Mostrar que o subconjunto { x 1 ,x 2 ,… ,x n } de vetores de um espaço vetorial V é L.D se, e somente se, existe um inteiro k ( 1 ≤ k ≤ n ) tal que x k é combinação linear dos demais vetores do conjun
Seja { u ,v ,w } um conjunto L.I de vetores de um espaço vetorial V . Provar que o conjunto { u + v - 3 w ,u + 3 v - w ,v + w ) é L.D.