Na Figura 9-4 (c), a aresta do cubo mede 3 e P é um ponto sobre H F tal que a medida angular entre D P → e D H → é 30 ° . Calcule as normas de D P → e H P → e a medida em radianos do ângulo P D ^ C .

D P → = 2 3 H P → = 3 m e dP D ^ C = arccos ⁡ 2 4

Enunciado

Álgebra Linear e Geometria Analítica - Paulo Boulos - Geometria Analítica - Ed: 3º - Capítulo 9.Exercício - Ex. 34

Na Figura 9-4 (c), a aresta do cubo mede e é um ponto sobre tal que a medida angular entre e é . Calcule as normas de e e a medida em radianos do ângulo .

Passo 1

Esse problema fica muito mais simples se usarmos uma base ortonormal. Note que a base não é ortonormal (é apenas ortogonal), pois seus vetores têm norma . Assim, vamos adotar uma base ortonormal , com

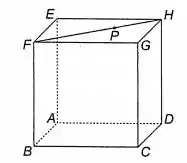
Nessa base, tomando como origem o ponto , o ponto tem coordenadas

Já os pontos e tem coordenadas

Assim,

Passo 2

O ângulo entre os vetores e é , de modo que

Fazendo o produto escalar:

Além disso,

Assim,

Desta forma,

Passo 3

Agora precisamos achar uma relação entre e para resolver o problema. Note que o ponto está sobre , de modo que

Como , temos que

Portanto,

Assim,

Portanto,

Assim, como , temos que

Por convenção, escolhemos :

Passo 4

Agora podemos calcular o que o problema pediu:

Para as normas:

Para achar o ângulo , temos que achar o ângulo entre os vetores e :

Assim,

Portanto,

Resposta

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

a) No exercício resolvido anterior, suponha que u → , v → e w → sejam não-nulos, não necessariamente unitários. Pode-se ainda concluir que ( u → ,v → ,w → ) é base?c) Mostre que, se u → , v → e w → sã

Sejam u → , v → , a → e b → vetores não0nulos tais que u → = α a → e v → = β b → . Mostre que a n gu → ,v → = a n ga → ,b → se α β0 e a n ga → ,b → = π - a n ga → ,b → se α β0 .

Prove que:a) u → + v → ⋅ u → - v → = u → 2 - v → 2 b) as diagonais de um paralelogramo são perpendiculares se, e somente se, o paralelogramo é um losango.c) v → u → + u → v → é ortogonal a v → u → - u

A medida angular em radianos entre u → e v → é π / 4 , u → = 5 e v → = 1 . Calcule a medida angular em radianos entre u → + v → e u → - v → .

Na Fig. 9-3, a circunferência de centro O tem raio r . Calcule B A → ⋅ B C → em função de r e das medidas α e β dos ângulos indicados. Aplique o resultado para provar que todo ângulo inscrito em uma c