Enunciado

Álgebra Linear e Geometria Analítica - Paulo Boulos - Geometria Analítica - Ed: 3º - Capítulo 9.Exercício - Ex. 61

Em relação a uma base ortonormal, sabe-se que e .

a) Verifique que , e são vértices de um triângulo.

b) Calcule o comprimento da altura relativa ao vértice e a área do triângulo .

Passo 1

O exercício forneceu dois vetores e no item (a) temos que ver se eles formam um triângulo. Para que os pontos , e sejam vértices de um triângulo, os vetores e devem ser LI.

Note que os vetores e não são paralelos, de modo que são LI. Desta forma, vemos que os três pontos são vértices de um triângulo.

Passo 2

Para resolver o item (b), vamos usar a figura:

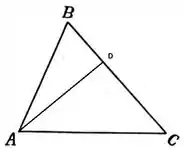
Nosso objetivo é procura o vetor , que representa a altura relativa ao vértice . Sabemos que

O vetor é dado por:

Vamos calcular a projeção:

Assim,

Portanto,

Passo 3

O comprimento da altura é a norma do vetor :

Para achar a área, basta lembrar que

Nessa caso, a base é a norma do vetor , que é :

Resposta

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Sejam u → = A B → e v → = A C → vetores não-nulos, de normas p e q , respectivamente. Prove que o vetor w → = q u → + p v → é paralelo à bissetriz de B Â C Â .

Prove que:a) 4 u → ⋅ v → = u → + v → 2 - u → - v → 2 b) u → ⋅ v → = 0 ⇔ u → + v → = u → + v → c) as diagonais de um paralelogramo têm comprimentos iguais se, e somente se, o paralelograma é um retângu

Prove que:a) u → + v → 2 + u → - v → 2 = 2( u → 2 + v → 2 ) b) a soma dos quadrados dos comprimentos das diagonais de um paralelogramo é igual à soma dos quadrado dos comprimentos dos quatro lados;c)

Prove que duas arestas opostas quaisquer de um tetraedro regular são ortogonais.

Prove que as coordenadas de qualquer vetor u → na base ortonormal B = i → ,j → ,k → são iguais aos produtos escalares de u → por i → , j → e k → , ou seja: u → = u → ⋅ i →i → + u → ⋅ j →j → + u → ⋅ k