Enunciado
Álgebra Linear e Geometria Analítica - Paulo Boulos - Geometria Analítica - Ed: 3º - Capítulo 9.Exercício - Ex. 36
A Figura 9-5 (a) mostra um paralelepípedo retângulo. Sendo e as medidas dos ângulos indicados e a medida de , mostre que
Passo 1
Vamos considerar primeiro a figura:
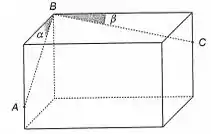
Para simplificar um pouco nossa vida, vamos considerar uma base ortonormal , ilustrada na figura:
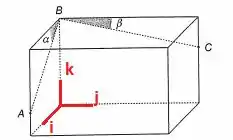
Vamos supor também que e .
Passo 2
Os vetores e podem ser escritos como:
Já o vetor :
Assim, o produto escalar entre eles será
Passo 3
Por fim, temos que relacionar isso com o ângulo , sabendo que
Como e :
Era isso que tínhamos que mostrar!
Resposta
Demonstração.
Exercícios de Livros Relacionados
Sendo u → e v → unitários, w → = 4 , u → ⋅ w → = - 2 , v → ⋅ w → = - 4 , e a n gu → ,v → = π / 3 , calcule: u → + v → + w → ⋅ u →
A Figura 9-4 (b) mostra um cubo. Sabendo que o comprimento de C M é o dobro do comprimento de G M , calcule a medida do ângulo B Â M Â .
Verdadeiro ou falso? Justifique sua resposta.a) u → ⋅ u → = 0 ⇔ u → = 0 → b) u → ⋅ v → = 0 ⇒ u → = 0 → o u v → = 0 → c) u → ⋅ v → - w → = u → ⋅ v → - u → ⋅ w → d) u → = - v → ⇒ u → ⋅ v → ≤ 0
Sendo u → e v → unitários, w → = 4 , u → ⋅ w → = - 2 , v → ⋅ w → = - 4 , e a n gu → ,v → = π / 3 , calcule: 2 u → - v → + w → ⋅ ( - u → + v → )
Sejam u → , v → e w → vetores de norma 1 tais que u → ⋅ v → = w → ⋅ v → = u → ⋅ w → = 1 / 2 . Verifique se w → é combinação linear de u → , v → .