Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Álgebra Linear e Geometria Analítica - Anton - Álgebra Linear- Ed: 10º - Capítulo 4.4 - Ex. 16

A figura dada mostra um sistema de coordenadas retangulares x y e um sistema de coordenadas x ' y ' com eixos oblíquos. Supondo que em todos os eixos foram utilizadas escalas de uma unidade, encontre as coordenadas x ' y ' dos pontos cujas coordenas x y estão dadas

a 1,1

b   1,0

c   0,1

d   a , b

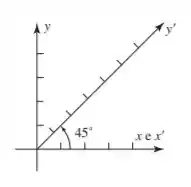
Passo 1

Desejamos encontrar os recíprocos dos pontos em x y para x ' y ' . Assim, devemos reparar que como os eixos estão transladados de um certo ângulo e teremos uma relação entre o sistema de coordenadas x y e x ' y ' que pode ser expresso por

F 1,0 = cos ⁡ α , s e n α

F 0,1 = cos ⁡ α ,   s e n α

Ou seja, para um dado ponto x ' , y ' vamos ter

F x ' , y ' = cos ⁡ α s e n α - s e n α cos ⁡ α ⋅ x ' y ' = x y

Para o caso do nosso exercício temos α = 45 ° o que transforma nossa relação para o seguinte formato

F x ' , y ' = 1 2 1 2 - 1 2 1 2 ⋅ x ' y ' = x y

Dessa forma, façamos o seguinte

L 1 + L 2 → L 2

E obteremos

1 2 1 2 0 2 ⋅ x ' y ' = x x + y

Daqui conseguimos extrair os correspondentes x ' e   y ' em função de x   e   y como sendo

y ' = x + y 2 ,   x ' = x - y 2

Passo 2

Pois agora ficou fácil converter de um sistema de coordenadas para outro, basta substituir os valores de x e y de cada ponto nas fórmulas encontrada acima. Então, para 1,1 teremos

x ' = 0 ,   y ' = 2 2 = 2

Já para 1,0 teremos

x ' = y ' = 1 2

Procedendo da mesma forma vamos encontrar para 0,1

x ' = - 1 2 ,   y ' = 1 2

Por fim, para a , b teremos

x ' = a - b 2 , y ' = a + b 2  

Pronto, está concluído nosso exercício.

Resposta

a 0 , 2

b 1 2 , 1 2

c - 1 2 , 1 2

d a - b 2 , a + b 2

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

a) Dados A = ( 2 ,5 ,3 ) e B = ( 1 ,1 ,0 ) , calvule as coordenadas dos pontos C e D , que determinam em A B três segmentos congruentes.b) Sejam A = ( x 1 ,y 1 ,z 1 ) , B = ( x 2 ,y 2 ,z 2 ) e X o pon
Se o sistema é ortogonal, quais são as coordenadas dos pontos simétricos de P = ( x ,y ,z ) em relação a cada plano coordenado.
Sejam A = ( 1 ,6 ,4 ) , B = ( 2 ,- 1 ,9 ) , C = ( 1 ,1 ,- 1 ) e D = ( 1 ,1 ,a ) . Para que valores de a esses pontos são vértices de um quadrilátero? Este quadrilátero é plano ou reverso?
O quadrilátero A B C D é convexo. Sabendo que 4C D → = - 3C A → + C B → , diga quais são suas diagonais e quais são seus lados.
Na Figura 13-3, A B C D E F G H é um paralelepípedo. Sejam e → 1 = A B → , e → 2 = A C → e e → 3 = A F → . Determine as coordenadas dos pontos A , B , C , D , E , F , G e H nos seguintes sistemas de c