Enunciado
Álgebra Linear e Geometria Analítica - Paulo Boulos - Geometria Analítica - Ed: 3º - Capítulo 13.Exercício - Ex. 16
O quadrilátero é convexo. Sabendo que , diga quais são suas diagonais e quais são seus lados.
Passo 1
Nesses exercício temos que identificar quais são os lados e quais são as diagonais de um quadrilátero com vértices em , , e . Para isso, vamos escrever primeiro
Assim, podemos desenhar a soma de com para obter :
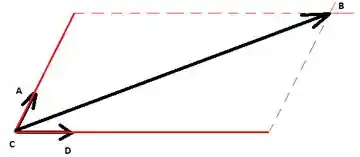
Passo 2
Fechando o quadrilátero :
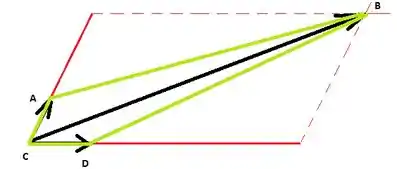
Assim, os lados são , , e . As diagonais são e .
Resposta
Os lados são , , e . As diagonais são e .
Exercícios de Livros Relacionados
Sejam os vetores v 1 = 1,0 , - 1 ,v 2 = 1,2 , 1 ev 3 = ( 0 , - 1,0 ) do I R 3 .Mostrar que B = v 1 ,v 2 , v 3 é base do I R 3 . Escrever e 1 = 1,0 , 0 ,e 2 = 0,1 , 0 ,e 3 = ( 0,0 , 1 ) como combinação
Seja A = { 3,2 x ,- x 2 } uma base de P 2 . Determinar o vetor-coordenada de v = 6 - 4 x + 3 x 2 em relação à base A.
No espaço vetorial I R 3 , consideremos a seguinte base: B = 1,0 , 0 ,0,1 , 0 ,1 , - 1,1 . Determinar o vetor coordenada de v ∈ I R 3 em relação à base B se: v = ( 2 , - 3,4 ) b) v = ( 3,5 , 6 ) c) v
Determinar o vetor coordenada de v = ( 6,2 ) em relação às seguintes bases α = 3,0 ,0,2 γ = { 1,0 ,0,1 } β = 1,2 ,2,1 δ = { 0,1 ,1,0 }
Como você pode reconhecer, pelas coordenadas, que um ponto pertence a um dos eixos coordenados? E a um dos planos coordenados?