Enunciado
Álgebra Linear e Geometria Analítica - Paulo Boulos - Geometria Analítica - Ed: 3º - Capítulo 13.Exercício - Ex. 9
a) Dados e , calvule as coordenadas dos pontos e , que determinam em três segmentos congruentes.
b) Sejam , e o ponto que divide na razão . Calcule as coordenadas de em função de e das coordenadas de e .
Passo 1
Vamos focar primeiro no item (a), com a imagem
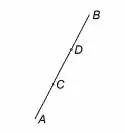
Devemos ter
Assim,
Como , temos que
Portanto,
Passo 2
Para achar a única mudança é
Assim,
Passo 3
Agora vamos para o item (b). Queremos achar o ponto que divide na razão :
Portanto,
Assim,
Resposta
Exercícios de Livros Relacionados
Dadas equações do conjunto Ω em relação a um dos sistemas de coordenadas ∑ 1 =O 1 , e 1 → , e 2 → , e 3 → e ∑ 2 = ( O 2 , f 1 → , f 2 → , f 3 → ) , obtenha equações de Ω em relação ao outro e identifi
Seja ∑ 2 o sistema obtido pela translação do sistema ortogonal ∑ 1 para um ponto O 2 pertencente a reta r : X = 1,0 , 1 + λ 1,4 , 2 ∑ 1 . Determine, em cada caso, as coordenadas de O 2 em relação a ∑
∑ 1 = O 1 , e 1 → , e 2 → , e 3 → e ∑ 2 = O 2 , f 1 → , f 2 → , f 3 → são dois sistemas de coordenadas tais que O 2 = 1,1 , 1 ∑ 1 e a matriz de mudança de base E = e 1 → , e 2 → , e 3 → para a base F
Adote o enfoque da observação anterior para escrever equações paramétricas de E 3 em relação ao sistema novo.
O ponto A = 2 , - 2 , 3 é um dos vértices de um cubo de centro P = 1 + 2 2 , 1 - 2 2 ,3 , que tem uma face contida no plano π 1 : x - y = 0 e outras duas paralelas ao plano π 2 : x + y - 2 z = 0 . Faç