Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Álgebra Linear e Geometria Analítica - Paulo Boulos - Geometria Analítica - Ed: 3º - Capítulo 13.Exercício - Ex. 7

Na Figura 13-3, A B C D E F G H é um paralelepípedo. Sejam e → 1 = A B → , e → 2 = A C → e e → 3 = A F → . Determine as coordenadas dos pontos A , B , C , D , E , F , G e H nos seguintes sistemas de coordenadas.

a) A ,   e → 1 ,   e → 2 , e → 3

b) ( H ,   e → 1 ,   e → 2 ,   e → 3 )

c) G ,   - e → 3 ,   e → 1 / 2 ,   2 e → 2

d) A ,   e → 2 ,   e → 3 ,   e → 1

Passo 1

Para nos guiar nesse problema, vamos considerar a figura 13-3:

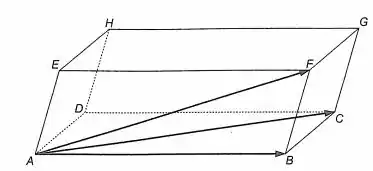
No item (a), a origem do sistema de coordenadas é

A = ( 0 ,   0 ,   0 )

Assim,

B = A + A B → ⇒ B = 0 ,   0 ,   0 + e → 1 ⇒ B = ( 1 ,   0 ,   0 )

C = A + A C → ⇒ C = ( 0 ,   1 ,   0 )

F = A + A F → ⇒ F = ( 0 ,   0 ,   1 )

Para o ponto D :

D = A + A D → = A + B C → = A + B A → + A C → = A - A B → + A C → = A -   e → 1 + e → 2 ⇒ D = ( - 1 ,   1 ,   0 )

Já para E :

E = A + A E → = E + B F → = A + B A → + A F → = A - A B → + A F → = A - e → 1 + e → 3 ⇒ E = ( - 1 ,   0 ,   1 )

Já para H :

H = E + E H → = A - A B → + A F → + B C → = A - A B → + A F → - A B → + A C →

Portanto,

H = A - 2   A B → + A C → + A F → = A - 2 e → 1 + e → 2 + e → 3 ⇒ H = ( - 2 ,   1 ,   1 )

Já para G :

G = H + H G → = H + A B → = A - 2   A B → + A C → + A F → + A B → = A - A B → + A C → + A F →

Assim,

G = A - e → 1 + e → 2 + e → 3 ⇒ G = ( - 1 ,   1 ,   1 )

Passo 2

No item (b) nós mudamos a origem do sistema de coordenadas para o ponto

H = ( 0 ,   0 ,   0 )

Note que no item (a) nós escrevemos todos os vetores com relação a A , e → 1 , e → 2 e e → 3 . Assim, vamos focar primeiro em achar as coordenadas de A para esse novo sistema de coordenadadas e depois usar os resultados do item anterior!

Vimos que

H = A - 2   A B → + A C → + A F →

Assim,

A = H + 2   A B → - A C → - A F → = H + 2 e → 1 - e → 2 - e → 3 ⇒ A = ( 2 ,   - 1 ,   - 1 )

Agora podemos achar todo o resto:

B = A + A B → = A + e → 1 ⇒ B = ( 3 ,   - 1 ,   - 1 )

C = A + A C → = A + e → 2 ⇒ C = ( 2 ,   0 ,   - 1 )

F = A + A F → = A + e → 3 ⇒ F = ( 2 ,   - 1 ,   0 )

Já o ponto D é

D = A -   e → 1 + e → 2 ⇒ D = ( 1 ,   0 ,   - 1 )

Para E :

E = A - e → 1 + e → 3 ⇒ E = ( 1 ,   - 1 ,   0 )

Por fim, para G :

G = A - e → 1 + e → 2 + e → 3 = ( 1 ,   0 ,   0 )

Passo 3

No item (c), o sistema de coordenadas é G ,   - e → 3 ,   e → 1 / 2 ,   2 e → 2 . Assim,

G = ( 0 ,   0 ,   0 )

Note que a ordem dos vetores na base foi alterada, cuidado com isso! Vamos achar o ponto A primeiro:

G = A - e → 1 + e → 2 + e → 3 ⇒ A = G + e → 1 - e → 2 - e → 3

Para deixar mais claro os vetores na nova base:

A = G + - e → 3 + 2 e → 1 2 - 1 2 2 e → 2 = 1 ,   2 ,   - 1 2

Agora que temos A , vamos achar os outros pontos:

B = A + e → 1 = A + 0   - e → 3 + 2 e → 1 2 + 0   2   e → 2 ⇒ B = 1 ,   4 ,   - 1 2

C = A + e → 2 = A + 0   - e → 3 + 0 e → 1 2 + 1 2   2   e → 2 ⇒ C = ( 1 ,   2 ,   0 )

D = A -   e → 1 + e → 2 = A + 0   - e → 3 - 2 e → 1 2 + 1 2   2   e → 2 ⇒ D = ( 1 ,   0 ,   0 )

E = A - e → 1 + e → 3 = A - 1   - e → 3 - 2 e → 1 2 + 0   2   e → 2 ⇒ E = 0 ,   0 ,   - 1 2

F = A + e → 3 = A - 1   - e → 3 + 0 e → 1 2 + 0   2   e → 2 ⇒ F = 0 ,   2 ,   - 1 2

H = A - 2 e → 1 + e → 2 + e → 3 = A - 1   - e → 3 - 4 e → 1 2 + 1 2   2   e → 2 ⇒ H = ( 0 ,   - 2 ,   0 )

Passo 4

Agora vamos fechar o problema com o item (d), cujo sistema é A ,   e → 2 ,   e → 3 ,   e → 1 . Aqui,

A = ( 0 ,   0 ,   0 )

Note que basta pegar as respostas do item (a) e inverter as coordenadas: a primeira vai para a terceira, a terceira para segunda e a segunda para primeira:

B = ( 0 ,   0 ,   1 )

C = ( 1 ,   0 ,   0 )

D = ( 1 ,   0 ,   - 1 )

E = ( 0 ,   1 ,   - 1 )

F = ( 0 ,   1 ,   0 )

G = ( 1 ,   1 ,   - 1 )

H = ( 1 ,   1 ,   - 2 )

Resposta

a) A = 0 ,   0 ,   0 ,                 B = 1 ,   0 ,   0 ,                 C = 0 ,   1 ,   0 ,                 D = - 1 ,   1 ,   0

E = - 1 ,   0 ,   1 ,                         F = 0 ,   0 ,   1 ,                       G = - 1 ,   1 ,   1                     e                 H = ( - 2 ,   1 ,   1 )

b) A = ( 2 ,   - 1 ,   - 1 ) ,                 B = ( 3 ,   - 1 ,   - 1 ) ,                 C = 2 ,   0 ,   - 1 ,                 D = 1 ,   0 ,   - 1

E = 1 ,   - 1 ,   0 ,                         F = 2 ,   - 1 ,   0 ,                       G = 1 ,   0 ,   0                     e                 H = ( 0 ,   0 ,   0 )

c) A = 1 ,   2 ,   - 1 2 ,                 B = 1 ,   4 ,   - 1 2 ,                 C = 1 ,   2 ,   0 ,                 D = 1 ,   0 ,   0

E = 0 ,   0 ,   - 1 2 ,                         F = 0 ,   2 ,   - 1 2 ,                       G = 0 ,   0 ,   0                     e                 H = ( 0 ,   - 2 ,   0 )

d) A = 0 ,   0 ,   0 ,                 B = 0 ,   0 ,   1 ,                 C = 1 ,   0 ,   0 ,                 D = 1 ,   0 ,   - 1

E = 0 ,   1 ,   - 1 ,                         F = 0 ,   1 ,   0 ,                       G = 1 ,   1 ,   - 1                     e                 H = ( 1 ,   1 ,   - 2 )

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Quais são as coordenadas do ponto simétrico P = ( x ,y ,z ) em relação à origem do sistema?
Se o sistema é ortogonal, quais são as coordenadas dos pontos simétricos de P = ( x ,y ,z ) em relação a cada eixo coordenado?
Sejam P = ( 1 ,- 1 ,2 ) , u → = ( 3 ,- 3 ,1 ) e v → = ( 1 ,1 ,1 ) . Obtenha a tripla de coordenadas de P - 2 u → + v → .
Sejam A = ( 3 ,0 ,- 1 ) , B = ( 0 ,3 ,0 ) , C = ( 5 ,1 ,- 2 ) e D = ( - 4 ,1 ,2 ) . Mostre que esses pontos são vértices de um trapézio e diga quais são as bases, os lados não-paralelos e as diagonais
Determine as coordenadas do ponto Q , simétrico de P = ( x ,y ,z ) em relação a M = x 0 ,y 0 ,z 0 .