Exercícios de Coordenada - Lista de Exercícios Resolvida
Questão 1
Seja um espaço vetorial e e duas bases distintas de .
Sejam e dois vetores distintos de .
Denotamos as coordenadas de em relação à base por .
Podemos sempre afirmar que:
Ver solução completa
Questão 3
- Existe alguma base de tal que, ?
- É possível encontrar uma segunda base também satisfazendo ?
Ver solução completaQuestão 4
No espaço vetorial de , consideraremos a seguinte base . Determinar as coordenadas de em relação à base se:
Questão 5
O conjunto é uma base do . Escreva o vetor genérico do como combinação linear de .
Ver solução completaQuestão 6
Seja um espaço vetorial e e duas bases distintas de .
Sejam e dois vetores distintos de .
Denotamos as coordenadas de em relação à base por .
Podemos sempre afirmar que:
Ver solução completa
Questão 7
Se as coordenadas de um vetor na base são , então as coordenadas de na base canônica são:
Ver solução completa
Questão 8
Considere um sistema de coordenadas em , em que é uma base ortonormal de . Sejam e considere os planos dados pelas equações
no sistema de coordenadas . Se for uma reta, então poderemos afirmar que:
a) e
b) e
c) e
d) e
e) e
Ver solução completaQuestão 9
Considere um sistema de coordenadas em , em que é uma base ortonormal de , e sejam e as retas dadas pelas equações:
e
no sistema de coordenadas Seja a reta que passa pelo ponto e que intersecta as retas e . Se for o ponto na intersecção de e , então será igual a:
a)
b)
c)
d)
e)
Ver solução completaQuestão 10
Calcule a primeira coordenada do vetor na base :
a)
b)
c)
d)
e) Não sei
Ver solução completaQuestão 11
Seja gerado por . Sabendo que uma base de possui dois elementos, assinale a resposta CORRETA:
Todos os conjuntos são linearmente independentes.
Um dos conjuntos é linearmente independente.
Um dos conjuntos é linearmente dependente.
Um dos conjuntos é linearmente dependente.
Ver solução completaQuestão 12
Seja um espaço vetorial de dimensão . Considere as seguintes afirmações:
Se é um subconjunto linearmente independente de , então podemos encontrar em , tal que é linearmente independente.
Todo subconjunto de com mais do que vetores é gerador de .
Qual das opções abaixo é CORRETA?
A afirmativa é falsa e é verdadeira.
A afirmativa é falsa e é falsa.
A afirmativa é verdadeira e é verdadeira.
A afirmativa é verdadeira e é falsa.
Ver solução completaQuestão 13
Seja uma base ortonormal de e considere os vetores e . Sejam tais que , com paralelo a e ortogonal a . Se , então é igual a
Ver solução completaQuestão 14
Seja uma base de e considere a base de , em que
Se , então a soma das coordenadas de em relação à base vale
Ver solução completaQuestão 15
Sejam vetores gerando um espaço vetorial .
Sejam , vetores linearmente independentes.
Assinale a alternativa VERDADEIRA:
Ver solução completa
Questão 16
Considere os planos e de equações cartesianas
(b) Considere o conjunto de vetores
os vetores que estão escritos na base canônica. Mostre que é uma base de .
(c) Considere o vetor v cujas coordenadas na base são
Determine as coordenadas de v na base canônica.
Ver solução completaQuestão 17
Considere o espaço vetorial dos polinômios com coeficientes reais e de grau até 2 e seja uma base de
- Seja Determine
- Seja tal que Determine
- Decida se a afirmação abaixo é verdadeira ou falsa. Se a afirmação for verdadeira, apresente uma demonstração. Se a afirmação for falsa, exiba explicitamente um contraexemplo.
Se então
Ver solução completaQuestão 18
Dentre os vetores abaixo, assinale aquele cuja soma das coordenadas na base é mínima.
(a)
(b)
(c)
(d)
Ver solução completaQuestão 19
Seja . Considere as afirmações.
(I) Existe um vetor não nulo tal que suas coordenadas na base canônica são o quádruplo de suas coordenadas na base .
(II) Existe um vetor não nulo tal que suas coordenadas na base canônica são o triplo de suas coordenadas na base .
(a) (I) é falsa e (II) é falsa.
(b) (I) é falsa e (II) é verdadeira.
(c) (I) é verdadeira e (II) é falsa.
(d) (I) é falsa e (II) é verdadeira.
Ver solução completaQuestão 20
Sejam e duas bases. Se , e e , determine as coordenadas de em relação à base .
Ver solução completaQuestão 21
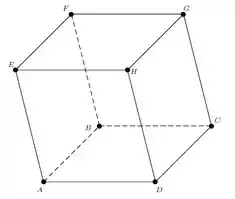
Considere os vetores , e no paralelepípedo da figura.
a) Justifique por que é uma base.
b) Determine as coordenadas do vetor na base .
c) Determine as coordenadas do vetor na base .
Questão 22
Considere um tetraedro e seja um ponto tal que
a) Explique por que pertence à face .
b) Mostre que as coordenadas de na face são .
Ver solução completaQuestão 23
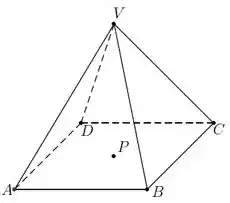
Em uma pirâmide regular tendo como base o quadrado e o vértice , considere a sequência de vetores e o ponto , projeção ortogonal do vértice na base da pirâmide.
a) Justifique por que é uma base.
b) Determine as coordenadas do vetor na base .
Questão 24
Sejam uma base de e os vetores e . Se as coordenadas na base destes vetores são e , então é:
a)
b)
c)
d)
e) Não sei.
Ver solução completaQuestão 25
Defina a base do . Se as coordenadas do vetor na base são , então o valor de é:
a) 11
b) 9
c) 10
d) 13
e) Não sei.
Ver solução completaQuestão 27
Qual dentre as proposições abaixo é VERDADEIRA?
Todo conjunto gerador de contém os vetores e .
O espaço gerado pelos vetores é .
O conjunto gerador de um espaço está contido em .
Cada vetor de pode ser escrito de forma única como combinação linear dos vetores e .
Ver solução completaQuestão 30
Seja o espaço dos polinômios de grau menor ou igual a 2.
A) Encontre a matriz de mudança de base da base para a base canônica , e a matriz mudança de base da base canônica para a base
B) Encontre as B-coordenadas do vetor .
Ver solução completaQuestão 31
Considere no espaço um trapézio ABCD, em que AB, BC, CD e AD são lados desse trapézio e os lados AD e BC são paralelos, como ilustrado na figura abaixo:

Seja M o ponto do segmento CD tal que . Suponha que:
E que as medidas dos ângulos e sejam iguais a . Seja um vetor não paralelo ao plano que contém o trapézio ABCD e considere a base
De . As coordenadas do vetor na base B são:
Ver solução completa
Questão 32
Seja uma base de e considere a base de , em que
Dado , as coordenadas de em relação à base são
a)
b)
c)
d)
e)
f)
g)
Ver solução completaQuestão 34
Seja o conjunto dos vetores de tais que a soma de suas duas primeiras componentes é igual a . Calcule a dimensão de :
Ver solução completa
Questão 35
Se as coordenadas de um vetor na base são , então as coordenadas de na base canônica são:
Ver solução completa
Questão 38
Suponha que queiramos escrever como combinação linear de e . Assinale a alternativa correta:
Encontraremos uma infinidade de possibilidades para os coeficientes dessa combinação.
Teremos uma única solução para os coeficientes dessa combinação.
Não encontraremos coeficientes para essa combinação linear.
Encontraremos duas possibilidades para os coeficientes dessa combinação.
Ver solução completaQuestão 39
Considere fixadas uma orientação no espaço e uma base ortonormal positiva de . Sejam e considere os vetores:
Se , então é igual a:
- ;
- ;
- ;
- ;
- .
Questão 40
Seja o conjunto dos polinômios da forma que satisfazem . A dimensão de é:
não está definida, pois não é subespaço.
Ver solução completaQuestão 41
Seja
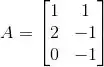
a matriz da transformação linear (em relação à base canônica). Se o vetor x tem coordenadas (1,1) em relação à base , então vale:
(a) (3,3,-1)
(b) (3,3,-2)
(c) (2,1,-1)
(d) (2,1,1)
Ver solução completaQuestão 42
Considere o ponto , o plano
E a reta
Se é o ponto de tal que , então a soma das coordenadas de é igual a:
Ver solução completa
Questão 43
Considere os vetores de cujas coordenadas na base canônica são
E o subespaço vetorial de gerado por estes vetores.
b) Determine uma base do subespaço formada com vetores do conjunto . Considere o vetor cujas coordenadas na base canônica são . Determine as coordenadas de na base .
Ver solução completaQuestão 44
Podemos afirmar que o conjunto-solução de tem dimensão igual a:
1
2
4
3
Ver solução completaQuestão 45
Considere os vetores de cujas coordenadas na base canônica são
E o subespaço vetorial de gerado por estes vetores.
d) Considere os vetores e cujas coordenadas na base canônica são
Determine para que
Seja uma base de tal que as coordenadas do vetor na base sejam
Ver solução completaQuestão 46
Considere fixada uma orientação em , e seja uma base ortonormal positiva de . Seja . A soma das coordenadas, em relação à base , do vetor que satisfaz
-
- é igual a
Ver solução completaQuestão 47
Se as coordenadas de um vetor na base são , então as coordenadas de na base canônica são:
Ver solução completa
Questão 49
Seja um paralelepípedo reto, com bases os quadrados e , de aresta , e arestas laterais , , , medindo .
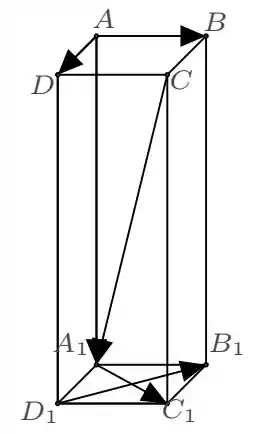
- Escreva os vetores , , como combinação linear dos vetores , e .
- Se são as coordenadas de na base , explique porque . Em seguida, calcule (corretamente!) a norma do vetor .
- Calcule o produto misto .
Questão 53
Seja fixada uma orientação no espaço . Considere as seguintes afirmações:
- Para quaisquer com não nulo, vale que é ortogonal a ;
- Se é uma base ortonormal de e se e , então ;
- Se e são bases negativas de e se e denotam as matrizes de mudança de base, então e .
Assinale a alternativa correta:
- apenas a afirmação (I) é verdadeira;
- apenas a afirmação (II) é verdadeira;
- todas as afirmações são verdadeiras;
- apenas as afirmações (I) e (II) são verdadeiras;
- apenas as afirmações (II) e (III) são verdadeiras.
Questão 54
Dizemos que duas matrizes comutam se satisfazem . Considere o conjunto de todas as matrizes que comutam com
Considere agora o caso particular das matrizes e .
Calcule a dimensão de .
Ver solução completaQuestão 55
Seja uma base de.
Se então a soma das coordenadas de na base é:
1
3
6
8
Ver solução completaQuestão 56
As coordenadas do vetor na base são . Calcule as coordenadas de na base canônica.
Ver solução completa
Questão 57
Classifique em verdadeira ou falsa as afirmativas:
Todo subconjunto linearmente independente de possui um número finito de vetores.
Todo subconjunto linearmente dependente de possui um número finito de vetores.
Qual das opções abaixo é CORRETA?
A afirmativa é falsa e é verdadeira.
A afirmativa é falsa e é falsa.
A afirmativa é verdadeira e é verdadeira.
A afirmativa é verdadeira e é falsa.
Ver solução completa