Enunciado
Álgebra Linear e Geometria Analítica - Paulo Winterle - Vetores e Geometria Analítica- Ed: 2º - Capítulo 8.Elipse - Ex. 15
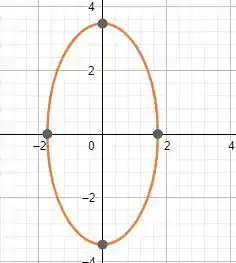
Focos e excentricidade
Passo 1
Sabemos que os focos são dados por quando a elipse está com o eixo menor em , então se teremos .
Outra informação dada é que a excentricidade é , então:
Multiplicando cruzado temos:
E com essas duas informações conseguimos encontrar com o teorema de Pitágoras:
A equação quando o eixo maior está em vai ser dada por:
Passo 2
A equação dessa elipse será dada por:
Onde os termos marcados em e marcado em .
Resposta
Exercícios de Livros Relacionados
A cada ponto P = x , y associemos o ponto P - = x - , y - , com x - = x a ,y - = y b , onde aeb são constantes não nulas. Quando P descreve a elipse x 2 a 2 + y 2 b 2 , mostre que P - descreve a circu
Cada uma das equações a seguir representa o conjunto vazio, um ponto, uma reta, um par de retas paralelas ou um par de retas que se cortam na origem. Decida cada situação e determine as retas, se for
No exercício anterior, quando é que as elipses se reduzem a circunferências?
Cada uma das equações a seguir representa o conjunto vazio, um ponto, uma reta, um par de retas paralelas ou um par de retas que se cortam na origem. Decida cada situação e determine as retas, se for
Identificar a cônica, achar a equação no último sistema de coordenadas. 2 1 x 2 + 6 x y + 13 y 2 - 132 = 0 ;