Enunciado
Álgebra Linear e Geometria Analítica - Paulo Winterle - Vetores e Geometria Analítica- Ed: 2º - Capítulo 8.Elipse - Ex. 11c
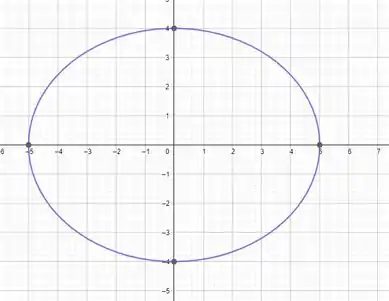
Esboçar o gráfico de uma elipse de excentricidade:
Passo 1
A primeira coisa que temos que ter em mente é que excentricidade é dada por:
Então:
Com isso, conseguimos definir que e , e com esses termos conseguimos aplicar no Teorema de Pitágoras da Elipse, que diz que:
Nossa equação pode ser dada por:
Passo 2
A equação dessa elipse será dada por:
Onde os termos marcados em e 4 marcado em .
Resposta
Exercícios de Livros Relacionados
Determine os eixos da elipse que é a imagem da circunferência unitária por cada uma das transformações lineares abaixo: b) T( x ,y )=( x+2 y ,3 x+2 y )
Determine os eixos da elipse que é a imagem da circunferência unitária por cada uma das transformações lineares abaixo: a) T( x ,y )=( x+2 y ,2 x+y )
Sejam FeF ' pontos não pertencentes a uma reta r . Usando Geometria Elementar, prove que existe um único ponto P em r que torna a soma d F , P + d ( P , F ' ) mínima. Ele é tal que os segmentos de ret
Prove que se a0 então a elipse x 2 a 2 + y 2 b 2 = 1 está contida no disco x 2 + y 2 ≤ a 2 e no retângulo x ≤ a ,y ≤ b , cujos vértices s˜ao os 4 pontos ( ± a , ± b ) . Prove também que todo ponto do
Prove que, dados a0 e b0 , quando t varia de 0a2 π o ponto p = ( acos t ,b sin t ) descreve uma elipse.