Enunciado
Álgebra Linear e Geometria Analítica - Alfredo Steinbruch e Paulo Winterle - Geometria Analítica- Ed: 1º - Capítulo 8.Problemas Propostos - Ex. 2a
Reduzir cada uma das equações à forma canônica, identificar e construir o gráfico da quadrática que ela representa.
Passo 1
O primeiro passo para reduzir uma equação na forma canônica é fazer com que o valor contido no segundo termo da igualdade seja .
Sendo a nossa equação :
Dividimos tudo por :
Simplificando:
O próximo passo é analisar as fórmulas propostas pelo livro no capítulo 8 e fazer uma comparação superficial , para dizer qual o tipo da nossa equação.
Passo 2
De acordo com o capítulo 8, nós temos aqui a equação de uma Elipse. Quando todos os coeficientes do primeiro termo da igualdade são positivos e e são números reais positivos, representam as medidas do semieixo elipsóide:
Dessa forma, nossa equação:
Trata-se de uma Elipse com: , , .
Passo 3
Os termos e são referentes a coordenada em que a elipse se encontra em cada um dos eixos. Isso significa que montaremos um gráfico em que , , que são como se fossem “raios” em cada um dos eixos.
Usando uma calculadora gráfica, como é o caso do Geogebra (online), teremos a seguinte elipse:
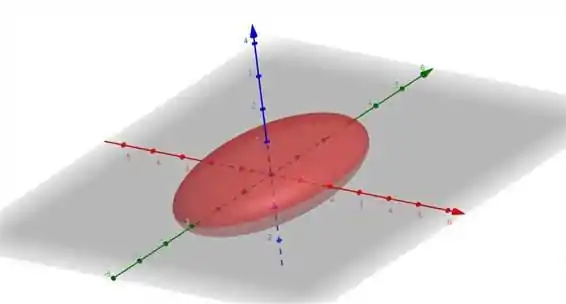
Já em 2D, para o plano xy temos o seguinte:
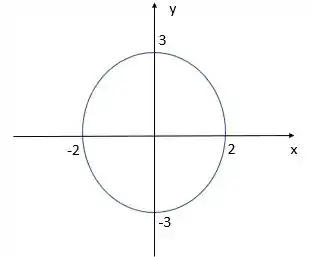
Ufa, agora terminamos!!
Resposta
Elipse,