Enunciado
Álgebra Linear e Geometria Analítica - Paulo Boulos - Geometria Analítica - Ed: 3º - Capítulo 23.Exercício - Ex. 8d
Identifique a cônica e, quando for o caso, obtenha seus parâmetros geométricos (, , ou ) e determine, em relação ao sistema inicial, os elementos geométricos principais: centro, focos, vértices, eixos, assíntotas, diretriz, etc.
(d)
Passo 1
(d) Agora queremos resolver essa equação aqui:
Nessa equação não aparece nenhum termo misto, então podemos simplesmente completar quadrados para resolver.
Começamos com os termos que dependem só de :
Dê uma olhada nesse produto notável:
Então se a gente somar dos dois lados da equação:
Podemos agrupar alguns termos:
Então:
Passo 2
Agora vamos fazer o mesmo para os termos que dependem de :
E vamos usar esse produto notável aqui:
Então, somando 3 dos dois lados:
Agora é só organizar um pouco:
Dividindo tudo por :
Que é a equação de uma elipse. Vamos tentar descobrir algumas das suas propriedades.
Passo 3
A forma geral da equação de uma elipse é:
Comparando com a nossa equação, logo podemos identificar alguns termos:
Quando a equação da elipse tem essa forma aqui:
Então o centro está no ponto . Comparando com a nossa equação, deduzimos que a posição do centro é:
E para calcular a posição dos vértices vamos fazer um desenho simples:
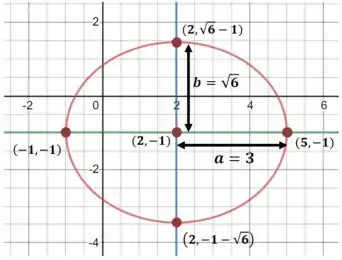
Além disso, os dois eixos da elipse são simplesmente as retas horitontal/vertical que passa pelo seu centro!
E por último podemos cacular os focos a partir do parâmetro que calculamos lá em cima.
Aqui é importante levar em consideração que o centro da elipse está deslocado por :
Pronto! Nossa elipse foi totalmente classificada.
Resposta
A equação descreve uma elipse com equação .