Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Álgebra Linear e Geometria Analítica - Anton - Álgebra Linear- Ed: 10º - Capítulo 4.9 - Ex. 27

O resultado enunciado no Exercício 26 pode ser estendido ao R 3 , isto é, pode ser provado que se A for uma matriz 3 × 3 de vetores coluna ortonormais e se , então a multiplicação por A é uma rotação em torno de algum eixo por algum ângulo θ . Use a Fórmula para mostrar que esse ângulo de rotação satisfaz a equação:

cos ⁡ θ = t r A - 1 2

Passo 1

Vamos lá! Primeiro temos que organizar algumas coisas antes de resolver essa questão.

Vamos começar lembrando da nossa matriz da formula 15 que expressa a rotação de um vetor v → = ( a ,   b ,   c ) no R 3 por um ângulo θ é dada por:

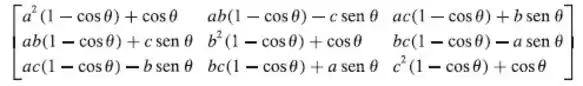
Agora vamos lembrar o que é o que ele apresenta na questão:

t r ( A ) , também conhecido como traço da matriz A é a soma dos elementos dos elementos da coluna principal da matriz:

Assim nosso t r ( A ) , para matriz apresentada fica:

t r A = a 2 1 - cos ⁡ θ + cos ⁡ θ + b 2 1 - cos ⁡ θ + cos ⁡ θ + c 2 1 - cos ⁡ θ + cos ⁡ θ

t r A = a 2 + b 2 + c 2 ⋅ 1 - cos ⁡ θ + 3 cos ⁡ θ

Passo 2

Agora, vamos retirar mais informações do nosso enunciado, ele diz que pra matriz da formula nossos vetores colunas serão ortonormais e , assim temos:

c 1 = a 2 1 - cos ⁡ θ + cos ⁡ θ a b 1 - cos ⁡ θ + c sen ⁡ θ a c 1 - cos ⁡ θ - b sen ⁡ θ

c 2 = a b 1 - cos ⁡ θ - c sen ⁡ θ b 2 1 - cos ⁡ θ + cos ⁡ θ b c 1 - cos ⁡ θ + b sen ⁡ θ

c 3 = a c 1 - cos ⁡ θ - b sen ⁡ θ b c 1 - cos ⁡ θ + a sen ⁡ θ c 2 1 - cos ⁡ θ + cos ⁡ θ

c 1 ⋅ c 2 = c 1 ⋅ c 3 = c 2 ⋅ c 3 = 0

Como nosso vetor v → = ( a ,   b ,   c ) é unitário:

a 2 + b 2 + c 2 = v → 2 = 1

Passo 3

Agora vamos escrever nosso t r ( A ) com as informações que obtemos:

t r A = a 2 + b 2 + c 2 ⋅ 1 - cos ⁡ θ + 3 cos ⁡ θ

Como a 2 + b 2 + c 2 = 1 :

t r A = 1 ⋅ ( 1 - cos ⁡ θ ) + 3 cos ⁡ θ

t r A = 1 - cos ⁡ θ + 3 cos ⁡ θ

t r A = 1 + 2 cos ⁡ θ

Isolando nosso cos ⁡ θ temos:

cos ⁡ θ = t r A - 1 2

Isso é tudo pessoal! Até a próxima!

Resposta

Ei, a resposta está no passo a passo :)

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Se a multiplicação por A gira um vetor x → do plano x y por um ângulo θ , qual é o efeito de multiplicar x → por A T ? Explique seu raciocínio.
Seja x 0 um vetor coluna não nulo em R 2 e suponha que T : R 2 → R 2 seja a transformação definida pela fórmula T x = x 0 + R θ x , em que R θ é a matriz canônica da rotação de R 2 em torno da origem
Nos Exercício, considere os operadores matriciais T A ∘T B das matrizes dadas. Encontre a matriz canônica de T A ∘T B . A = 6 3 - 1 2 0 1 4 - 3 6 B = 4 0 4 - 1 5 2 2 - 3 8
Encontre a matriz canônica para a composição dada em R 3 para uma projeção ortogonal sobre o plano x y , seguida de uma reflexão no plano y z .
Encontre a matriz canônica para a composição dada em R 3 para uma reflexão no plano y z , seguida de uma projeção ortogonal sobre o plano x z .