Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Álgebra Linear e Geometria Analítica - Anton - Álgebra Linear- Ed: 10º - Capítulo 4.9 - Ex. 28

Seja A uma matriz 3   ×   3   (diferente da matriz identidade) que satisfaça as condições enunciadas no Exercício 27 . Pode ser mostrado que se x for um vetor não nulo qualquer em R 3 , então o vetor u =   A x +   A T x +   1 -   t r A x   determina um eixo de rotação quando u for posicionado com seu ponto inicial na origem. [Ver o artigo The Axis of Rotation: Analysis, Algebra, Geometry, por Dan Kalman, em Mathematics Magazine, Vol. 62 , N º   4 , outubro de 1989 .]

  1. Mostre que a multiplicação por

    2. A = 1 9 - 4 9 8 9 8 9 4 9 1 9 - 4 9 7 9 4 9

    É uma rotação.

  2. Encontre um vetor de comprimento 1 que define um eixo da rotação.

  3. Encontre todas as soluções da equação do Exercício 27 que pertençam ao intervalo [ 0 ,   2 π ] e, substituindo essas soluções na fórmula ( 15 ) , encontre um ângulo de rotação em torno do eixo da parte ( b ) que resulta da multiplicação pela matriz A da parte ( a ) .

Passo 1

  1. Vamos lá! Essa questão é tipo ENEM, o enunciado não serve pra nada além de te desorientar! Exceto pelo artigo de referência! (-_-) tendo isso em mente vamos nos focar nas nossas letras!

    Agora tendo isso em mente, vamos relembrar da nossa matriz da formula 15 , que é dada por:

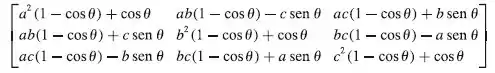
    Agora vamos comparar com a nossa matriz A :

    A = 1 9 - 4 9 8 9 8 9 4 9 1 9 - 4 9 7 9 4 9

    Assim temos: que t r A = 1 , logo:

    ( 1 - cos ⁡ θ ) ⋅ a 2 + b 2 + c 2 + 3 cos ⁡ θ = 1

    Se fizermos θ = π 2 , temos:

    a 2 + b 2 + c 2 = 1

    Substituindo os valores de θ nos itens de t r ( A ) temos:

    a 2 1 - cos ⁡ θ + cos ⁡ θ = a 2 = 1 9

    b 2 1 - cos ⁡ θ + cos ⁡ θ = b 2 = 4 9

    c 2 1 - cos ⁡ θ + cos ⁡ θ = c 2 = 4 9

    Assim: a = 1 3 ,   b = 2 3 , c = 2 3

    Logo nossa matriz A se trata de uma rotação por um ângulo de π 2 sofrida por um vetor:

    v → = 1 3 , 2 3 , 2 3 .

    Passo 2

  2. Para um vetor de dimensão 1 o artigo sugere que esse vetor seja:

    e = a 31 + a 13 a 32 + a 23 1 + a 33 - a 22 - a 11

    Vamos nossa matriz padrão de rotação do eixo z R 3 :

    cos ⁡ θ - sen ⁡ θ 0 sen ⁡ θ cos ⁡ θ 0 0 0 1

    0 0 1 + 1 - cos ⁡ θ - cos ⁡ θ = 0 0 2 - 2 cos ⁡ θ

    Como nossa matriz deve ser unitária temos que:

    2 - 2 cos ⁡ θ = 1

    Logo os únicos ângulos possíveis pra isso no intervalo [ 0 ,   2 π ] são:

    π 3   e 5 π 3

    Assim nossa matriz fica:

    S = 1 2 - 3 2 0 3 2 1 2 0 0 0 1

    Passo 3

Se olharmos com carinho o enunciado ele nos diz que ele quer um ângulo θ que atenda a equação:

cos ⁡ θ = t r A - 1 2

E que esteja contido no intervalo de 0 ,   2 π .

Mas contanto que nosso vetor v → = ( a ,   b ,   c ) seja unitário todos os ângulos entre 0 ,   2 π atendem esse pré-requisito.

Como ele quer um ângulo de rotação pela matriz:

S = 1 2 - 3 2 0 3 2 1 2 0 0 0 1

Pela matriz A .

A = 1 9 - 4 9 8 9 8 9 4 9 1 9 - 4 9 7 9 4 9

Como nosso ângulo deve atender a regra:

cos ⁡ θ = t r S ⋅ A - 1 2

Então temos que nos preocupar somente com a diagonal principal da nossa matriz S ⋅ A :

t r S ⋅ A = 1 2 ⋅ 1 9 - 3 2 ⋅ 8 9 + 3 2 ⋅ - 4 9 + 1 2 ⋅ 4 9 + 4 9

t r S ⋅ A = - 0,43247831

Agora podemos calcular nosso θ .

cos ⁡ θ = - 0,43247831 - 1 2 = - 0,71623915

cos - 1 ⁡ - 0,71623915 = 135,7448449 °

θ ≅ 3 π 4

Resposta

  1. Vide questão

  2. S = 1 2 - 3 2 0 3 2 1 2 0 0 0 1

  3. θ ≅ 3 π 4
Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Encontre a matriz canônica para a composição dada em R 2 para uma projeção ortogonal sobre o eixo y seguida de uma contração de fator k = 1 2 .
Encontre a matriz canônica para a composição dada em R 2 para uma reflexão sobre o eixo x seguida de uma dilação de fator k = 3 .
Encontre a matriz canônica para a composição dada em R 3 para uma rotação de 30 ° em torno do eixo x , seguida de uma rotação de 30 ° em torno do eixoz , seguida de uma contraçãode fator k = 1 4
Determine se T 1∘ T 2 =T 2 ∘T 1 . T 1:R 2→R 2 é a projeção ortogonal sobre o eixo x e T 2:R 2→R 2 é a rotação por um ângulo θ
Determine se T 1∘ T 2 =T 2 ∘T 1 . T 1:R 3→R 3 é a rotação em torno do eixo x por um ângulo θ:R 3→R 3 é arotação em torno do eixo z por um ângulo θ .