Enunciado
Álgebra Linear e Geometria Analítica - LIMA, Elon L. Geometría analítica e Álgebra Linear- Ed: 2º - Capítulo 24.Problemas - Ex. 4a
Identifique geometricamente os seguintes conjuntos
Passo 1
Oiiii, gente! Vamos para mais uma?!
Bom primeiro vamos dar uma olhadinha na nossa equação de 2° grau, vemos que só a coordenada z está sendo utilizada né, então já conseguimos pensar em uma figura contida em um plano. Como não temos um y ou um x em função de z , então é notável que a figura não só está contida no plano, como de fato é o próprio plano z.
Passo 2
Resolvendo a equação de 2° grau por meio da fórmula de bhaskara, temos:
Logo, é o plano z = 1.
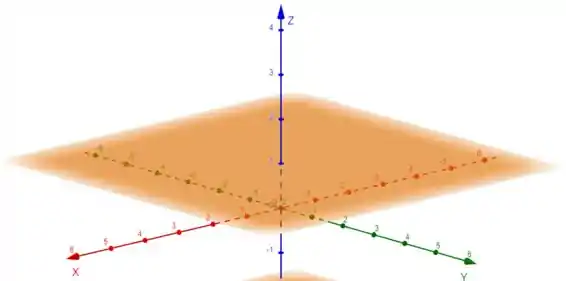
Tudo ok? Bora pra mais uma!
Bons Estudos!
Resposta
Plano z= 1
Exercícios de Livros Relacionados
Determine a equação do plano constituído de todos os pontos que são equidistantes dos pontos ( 2 , 5,5 ) e ( - 6,3 , 1 ) .
Determine as equações paramétricas da reta que passa pelo ponto ( 0 , 1,2 ) , é paralela ao plano x + y + z = 2 e perpendicular à reta x = 1 + t , y = 1 - t , z = 2 t .
Determine a equação do plano constituído de todos os pontos que são equidistantes dos pontos ( 1 , 0 , - 2 ) e ( 3,4 , 0 ) .
Determine as equações paramétricas da reta que passa pelo ponto ( 0 , 1,2 ) , é perpendicular à reta x = 1 + t , y = 1 - t , z = 2 t , e intercepta essa reta.
Quais das quatro retas seguintes são paralelos? Existem duas coincidentes? L 1 : x = 1 + t ,y = t ,z = 2 - 5 t L 2 : x + 1 = y - 2 = 1 - z L 3 :x = 1 + t ,y =4 + t ,z = 1 - t L 4 : r → = 2,1 , - 3 + t