Enunciado
Álgebra Linear e Geometria Analítica - LIMA, Elon L. Geometría analítica e Álgebra Linear- Ed: 2º - Capítulo 24.Problemas - Ex. 4c
Identifique geometricamente os seguintes conjuntos
Passo 1
Oiiii, gente!
Bom, primeiro vamos dar uma olhadinha na nossa equação, vemos que são utilizadas as coordenadas x e z, logo independe do y.
Resolvendo essa equação, temos:
Dessa forma, vamos fazer a representação do primeiro plano:
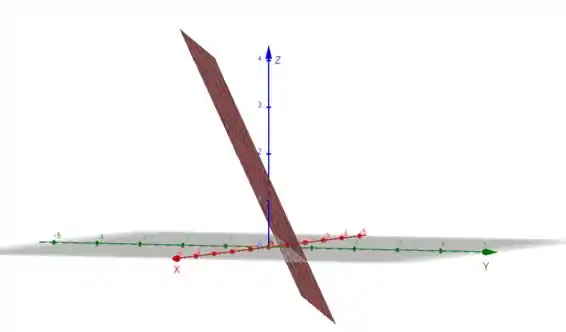
Passo 2
Agora, vamos fazer a representação do segundo plano:
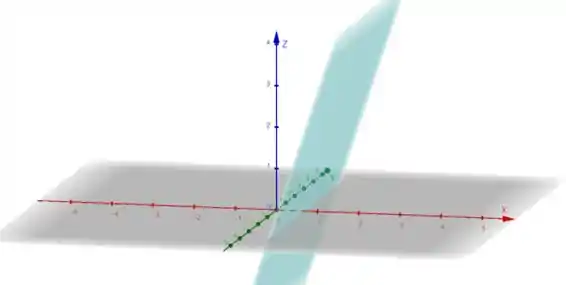
Passo 3
E por fim, juntando essas duas representações temos o gráfico desejado:
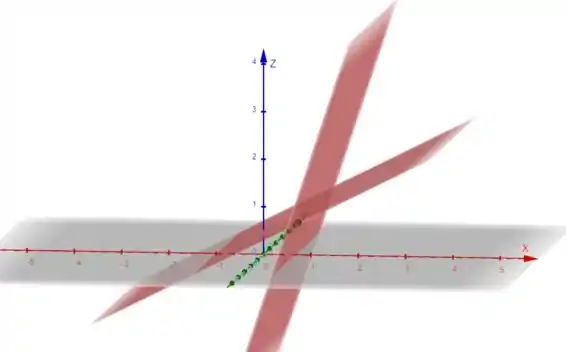
Tudo certinho? Bora fazer as outras letrasss!
Bons Estudos!
Resposta
Ei, a resposta está no passo a passo :)
Exercícios de Livros Relacionados
Escreva uma equação vetorial e equações paramétricas do plano π , utilizando as informações dadas em cada caso.a) π contém A = ( 1 ,2 ,0 ) e é paralelo aos vetores u → = ( 1 ,1 ,0 ) e v → = ( 2 ,3 ,-
Obtenha equações paramétricas do plano que contém o ponto A = ( 1 ,1 ,2 ) e é paralelo ao plano π :x = 1 + λ + 2 μ y = 2 λ + μ z = - λ
Decomponha u → = ( 1 ,2 ,4 ) como soma de um vetor paralelo à reta r : X = 1 ,9 ,18 + λ ( 2 ,1 ,0 ) com outro paralelo ao plano π :x = 1 + λ y = 1 + μ z = λ - μ
São dados os sistemas de equações x = λ + 2 μ y = 1 + λ + 2 μ z = - λ - 2 μ x = x 0 + λ a + μ m y = y 0 + λ b + μ n z = z 0 + λ c + μ p a) Descreva o lugar geométrico dos pontos X = ( x ,y ,z ) que sa
Obtenha equações paramétricas dos planos coordenados.