Com a notação e o resultado do exercício anterior, chamando de F o foco e P0 o pé da perpendicular baixada de P sobre a diretriz, mostre que o quadrilátero PP0P′ F é um losango. Conclua que a tangente por P é a bissetriz do ângulo P0PF

Olá galera! tudo bem?

Bora junto resolver mais um problema!

Esse é exercício é totalmente algébrico pois se trata de uma demonstração. Beleza!

Preparado?

Antes você deve lembrar que na questão anterior provamos que o ponto que pertence a parábola e o ponto que pertence a uma reta tangente são equidistante beleza!

Vamos começar então!

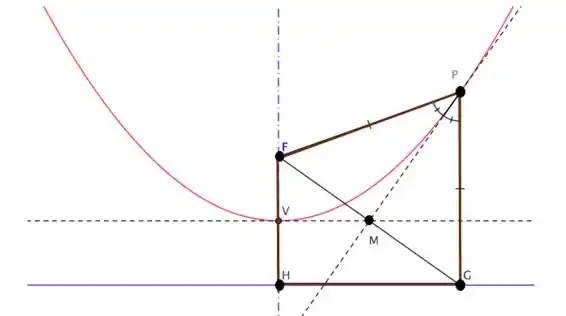
Neste problema vamos considerar como o foco da parábola, e sua diretriz, com vértice no ponto médio de . Da definição de parábola temos que .

Onde é qualquer ponto da parábola e sua projeção na diretriz.

A tangente em é a bissetriz do ângulo de , portanto, é perpendicular à base do triângulo isósceles , e o intercepta em seu ponto médio .

Mas a tangente em é paralelo à diretriz e bissetriz , portanto, também corta no , conforme podemos observar na imagem abaixo, assim como a formação de um losango .

Prontinho, acabamos te vejo na próxima questão!