Enunciado
Álgebra Linear e Geometria Analítica - Paulo Boulos - Geometria Analítica - Ed: 3º - Capítulo 22.Exercício - Ex. 65
Um dos lados de um retângulo circunscrito a elipse é paralelo a reta de equação . Determine os vértices do retângulo.
Passo 1
A equação dessa elipse pode ser escrita como:
E as equações das retas tangentes podem ser escritas como:
Com sendo pontos de tangência. E como essas retas são paralelas a , então temos que por proporcionalidade que:
Então , logo equações de reta tangente serão dadas na forma de:
E como esse ponto pertence a elipse então:
Logo
Esses serão todos os pontos de tangência com a elipse
Isso para a família de retas que tem uma cara igual a
Passo 2
E temos retas paralelas a formando os lados do quadrado então para um ponto como teremos uma reta igual a:
E se aplicarmos o ponto , nós teremos uma reta igual a:
E como temos um retângulo, então temos que os outros dois lados que faltam descobrir tem equações de reta perpendiculares a família de retas e para isso esse outro lado terá uma equação da cara de (já que a multiplicação dos coeficientes angulares de duas retas perpendiculares é de ), portanto os pontos de tangência para essas retas serão de:
Então , logo equações de reta tangente serão dadas na forma de:
E como esse ponto pertence a elipse então:
Logo
Então os pontos de tangência serão e , o que nos darão equações de retas iguais a:
E o ponto de encontro das retas não paralelas são:
Que são os vértices do nosso quadrado tal como mostra a figura.
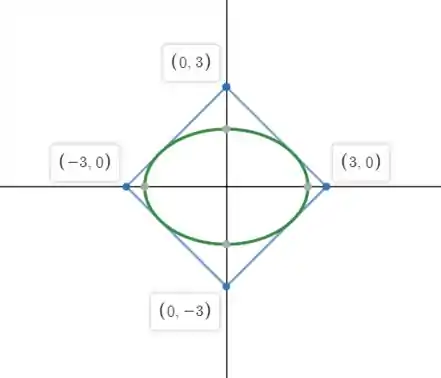
O que nos dá um quadrado.