Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Álgebra Linear e Geometria Analítica - Paulo Boulos - Geometria Analítica - Ed: 3º - Capítulo 22.Exercício - Ex. 78

Obtenha equações das retas que contém o ponto P = ( 1 , - 9 ) e são tangentes a hipérbole de equação 3 x 2 - y 2 = 39 . Determine os pontos de tangência e a reta normal em cada um deles.

Passo 1

A equação da reta tangente tem a seguinte forma:

h x p + k y q = 1

Onde ( h , k ) é o ponto de tangência e p e q serão dadas por:

x 2 p + y 2 q = 1 → x 2 13 - y 2 39 = 1

Então p = 13 e q = - 39 , logo:

h x 13 - k y 39 = 1

E podemos aplicar o ponto x , y = ( 1 , - 9 ) nessa equação pois ele pertence a essa reta.

h 13 + 9 k 39 = 1

Logo:

h 13 = 1 - 9 k 39 = 39 - 9 k 39

h = 39 - 9 k 3

E como h e p pertencem a hipérbole nós teremos:

h 2 p + k 2 q = 1

h 2 13 - k 2 39 = 1

As duas equações (que estão emolduradas) nos darão pontos iguais a:

k 1 = 3 ; k 2 = 6

Portanto:

h 1 = 39 - 9 ⋅ 3 3 = 4 ;           h 2 = 39 - 9 ⋅ 6 3 = - 5

Então os pontos de tangência serão:

h 1 , k 1 = ( 4,3 )

h 2 , k 2 = ( - 5,6 )

Passo 2

Já para achar a equação da reta tangente, bem... nós temos o ponto ( 1 , - 9 ) e os pontos de tangência. Começando pelo ponto de tangência ( 4,3 ) nós podemos aplicar esse ponto na equação da reta igual a:

y = m x + c

E que vai dar

3 = 4 m + c

Agora aplicando ( 1 , - 9 ) teremos:

- 9 = m + c

Diminuindo a primeira da segunda nós teremos:

9 + 3 = 3 m → m = 4

Portanto:

- 9 = 4 + c → c = - 13

Então a primeira reta tangente terá equação de:

y = 4 x - 13

Passo 3

Agora aplicando o ponto ( - 5,6 ) na equação y = m x + c

6 = - 5 m + c

Com um sistema com:

- 9 = m + c

Por conta do ponto ( 1 , - 9 ) nós teremos:

- 9 - 6 = 5 m + m → m = - 2.5

Portanto:

- 9 = - 2.5 + c → c = - 6.5

Então a equação fica:

y = - 2.5 x - 6.5

Multiplicando tudo por 2 teremos:

2 y = - 5 x - 13

Uma forma melhor de escrever talvez seja:

5 x + 2 y + 13 = 0

Passo 4

A reta normal é uma reta que está perpendicular a reta tangente portanto o coeficiente angular das duas retas seguem a seguinte regra:

m t a n g ⋅ m n o r m a l = - 1

Portal o coeficiente angular da reta normal na primeira equação de fórmula igual a y = 4 x - 13   , terá um valor de:

4 ⋅ m n = - 1

m n = - 1 4

Portanto ela terá uma cara igual a:

y = - x 4 + c

E essa equação também se encontra com o ponto ( 4,3 ) , então:

3 = - 4 4 + c → c = 4

Então:

y = - x 4 + 4

4 y = - x + 16

Pra ter uma melhor visualização nós teremos o seguinte gráfico com as duas retas:

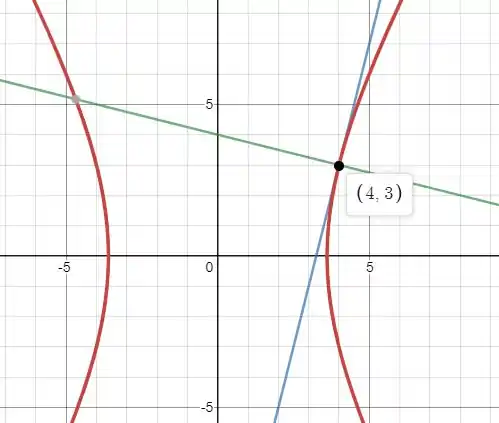
Passo 5

Agora a reta normal para 5 x + 2 y + 13 = 0

No ponto   ( - 5,6 ) :

Essa equação pode ser escrita como:

y = - 5 2 x - 13 2

Portanto a equação da reta normal pode ser escrita como:

y = 2 5 x + c

Se aplicarmos o ponto   ( - 5,6 ) nós teremos:

6 = - 2 5 ⋅ 5 + c

6 = - 2 + c

c = 8

Então a equação da reta normal será:

y = 2 5 x + 8

E o gráfico dessas duas retas serão:

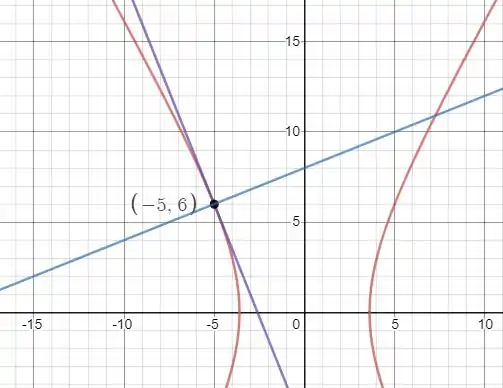
Resposta

Pontos de tangência:

h 1 , k 1 = ( 4,3 )

h 2 , k 2 = ( - 5,6 )

Retas tangentes:

y = 4 x - 13

5 x + 2 y + 13 = 0

Retas normais:

4 y = - x + 16

y = 2 5 x + 8

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Determinar uma equação da curva descrita por um ponto que se move, de modo que sua distância ao ponto A ( - 1 ,3 ) seja:b) o dobro de sua distância à reta x=3 ;
Determinar uma equação da curva descrita por um ponto que se move, de modo que sua distância ao ponto A ( - 1 ,3 ) seja:b) a metade de sua distância à reta x=3 ;
Encontrar uma equação de hipérbole com focos nos vértices da elipse x 2 25 + y 2 9 = 1 e vértices nos focos dessa elipse.
13. Esboçar o gráfico de uma hipérbole (com suas assíntotas) de centro 0 ,0 , eixo real sobre O x e excentricidade:c) 2
Em cada um dos problemas de 1 a 12 , esboçar o gráfico e determinar os vértices, os focos, a excentricidade e as equações das assíntotas das hipérboles dadas.2. y 2 4 - x 2 9 = 1