Enunciado
Álgebra Linear e Geometria Analítica - Paulo Boulos - Geometria Analítica - Ed: 3º - Capítulo 22.Exercício - Ex. 64
Conhecendo o vértice de um paralelogramo circunscrito a elipse , determine os outros três.
Passo 1
Basicamente queremos formar uma imagem como essa aqui.
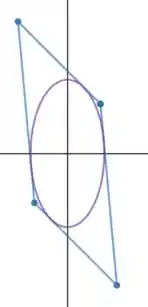
E como vimos na questão , se um ponto é pertencente a uma reta tangente a elipse então existe um ponto que também será tangente a essa elipse. Pois forma-se uma reta colinear entre esses dois pontos e o ponto de origem do sistema cartesiano. Portanto um dos vértices desse paralelogramo será:
Mesmo que o ponto só esteja na reta tangente e não seja um ponto de tangência em si.
Passo 2
Essa equação de elipse se dividindo tudo por pode ser escrita como:
E como podemos ver na figura um ponto de vértice do paralelogramo se liga a duas retas tangentes a elipse e dizendo que temos pontos de tangencia em logo:
Para:
Então se substituímos o ponto na primeira equação nós teremos uma equação de reta igual a:
Por esse sistema nós vemos que teremos pontos de tangência em :
Esses dois pontos de tangência nos darão duas equações de reta tangentes a elipse
Passo 3
Essas retas tangentes serão iguais a:
Para os pontos e teremos a reta com coeficiente angular igual a:
E coeficiente linear igual a:
Portanto temos uma reta tangente igual a
E a outra reta tangente entre e terá coeficiente angular em:
E coeficiente linear igual a:
Logo teremos uma equação de reta tangente em:
Essas retas terão como ponto de encontro o ponto tal como pode ser visto na imagem a baixo:
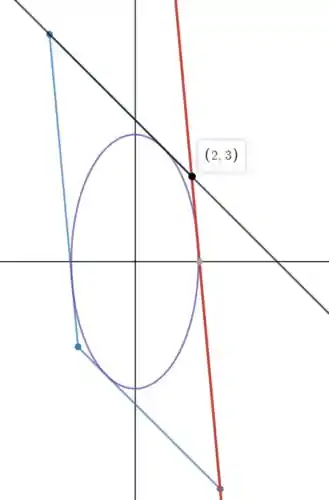
Passo 4
Então para encontrarmos um dos pontos de vértice que faltam basta encontrarmos a equação de uma das retas do paralelogramo que faltam e que será oposta e simétrica a uma das outras retas previamente já encontradas, por exemplo pegando a reta:
Nós temos que a outra reta paralela a ela será dada por:
Nos dando a figura abaixo
E o ponto de união entre:
E
Será:
Então o outro vértice que falta será a parte espelhada em e desse último ponto e que será: