Enunciado
Álgebra Linear e Geometria Analítica - Alfredo Steinbruch e Paulo Winterle - Geometria Analítica- Ed: 1º - Capítulo 3.Problemas Propostos - Ex. 14
Os lados de um triângulo retângulo (reto em ) medem 5, 12 e 13. Calcular
Passo 1
Para acharmos o produto escalar entre os pares de vetores, vamos usar
Passo 2
Como esse triângulo é reto em , então
Passo 3
Se desenharmos o triângulo,
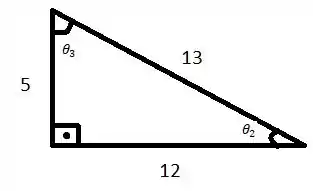
Vemos que a hipotenusa é o maior lado, 13. Então, os cossenos dos ângulos e são as razões dos lados 5 e 13 e 12 e 13.
Passo 4
Agora, vamos colocar na relação e encontrar a resposta
Resposta
Exercícios de Livros Relacionados
Se r t = ( e 2 t ,e - 2 t , t e 2 t ) , determine T 0 ,r ' ' ( 0 ) e r ' t ⋅ r ' ' ( t ) .
Para os vetores do Exercício 40, determine p e r p a b e ilustre esboçando os vetores a ,b ,p r o j a b e p e r p a b . a = ( 1 , 4 ) b = ( 2,3 )
Determine os cossenos diretores e os ângulos diretores do vetor.Forneça o ângulo diretor com precisão de um grau.c , c , c Onde c0
Se um vetor tem ângulos diretores α = π 4 e β = π 3 , determine o terceiro ângulo diretor γ .
Prove que u ∙ v =± u v se, e somente se, um dos vetores u, v é múltiplo do outro. Em seguida, compare u + v 2 = ( u + v∙ u + v ) com u + v 2 para concluir que u + v = u + | v | se, e somente se, um do