Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Álgebra Linear e Geometria Analítica - Vetores e uma iniciacao a geometria analitica mello e watanabe- Ed: 2º - Capítulo 6.Exercícios Propostos - Ex. 3

Losango é um paralelogramo cujos lados têm a mesma medida e as diagonais são perpendiculares. A , B , C e D são os vértices consecutivos de um losango. A   =   ( - 1 , - 1,0 ) , B =   ( 1,4 , a ) e C   =   ( 3,1 , 2 ) . Determine a e as coordenadas do vértice D .

Passo 1

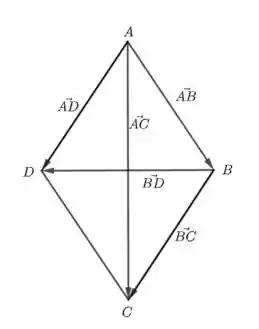
Vamos começar essa questão identificando alguns dos vetores com os pontos que já temos:

A B → = B - A = ( 1,4 , a ) - ( - 1 , - 1,0 ) = ( 2,5 , a )

A C → = C - A = ( 3,1 , 2 ) - ( - 1 , - 1,0 ) = ( 4,2 , 2 )

C B → = B - C = ( 1,4 , a ) - ( 3,1 , 2 ) = ( - 2,3 , a - 2 )

Passo 2

Usando as regras de soma vetorial, podemos calcular:

B D → = B A → + B C → = - A B → - C B → = - ( 2,5 , a ) - ( - 2,3 , a - 2 ) = ( 0 , - 8,2 - 2 a )

Por outro lado, temos

B D → = D - B

⇒ D = B D → + B = ( 0 , - 8,2 - 2 a ) + ( 1,4 , a ) = ( 1 , - 4,2 - a )

Agora, só precisamos determinar o valor de a .

Passo 3

As diagonais A C → e B D → devem ser ortogonais, então

A C → ⋅ B D → = 0

⇒ ( 4,2 , 2 ) ⋅ ( 0 , - 8,2 - 2 a ) = 0

⇒ - 16 + 4 - 4 a = 0

⇒ - 12 = 4 a ⇒ a = - 3

Agora, substituímos esse valor na equação do ponto D :

D = ( 1 , - 4,2 - a ) = ( 1 , - 4,5 )

Resposta

a = - 3

D = ( 1 , - 4,5 )

Exercícios de Livros Relacionados

Obtenha os pontos da reta r que equidistam de A e B e comente as peculiaridades geométricas de cada caso.b) r : X = 0 ,0 ,4 + λ ( 4 ,2 ,- 3 )A = 2 ,2 ,5B = ( 0 ,0 ,1 )
Se Ax² + Ay² + Dx + Ey + F = 0 é a equação de uma circunferência, quais são as coordenadas do centro?
São dados os pontos: A=( 5 , - 3,1 ) , B=( - 2,4 , 3 ) e C=( 3,1 , - 4 ) . Determine os pontos médios M de B C ̄ , N de A B ̄ e Q de A C ̄ .Determine as coordenadas do ponto P de A M ̄ tal que A P̄ =2
A , B , C e D são vértices consecutivos de um paralelogramo, sendo A=( 1 , - 3,2 ) , B =( 0,6 , - 3 ) e C=( 5,1 , 4 ) .Determine as coordenadas do ponto D Mostre que as diagonais A C → e B D → têm o m