(a) Mostramos no Exemplo 1 que os vetores mutuamente ortogonais e formam um conjunto linearmente independente de vetores em . Será que qualquer conjunto de vetores mutuamente ortogonais em forma um conjunto linearmente independente? Justifique sua conclusão geometricamente.
(b) Justifique sua conclusão algebricamente. [Sugestão: use produto escalar.]
Passo 1
-
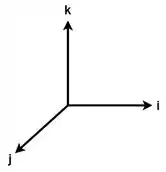
Independente, do sentindo e do módulo dos vetores, se eles são ortogonais entre si eles não se projetam entre si, por isso o conjunto que os contém é linearmente independente.
Passo 2
Tendo vetores vamos fazer a combinação linear entre os 3.
Sendo nosso conjunto não nulo, logo é L.I.
Resposta
Ei, a resposta está no passo a passo :)