Enunciado

Álgebra Linear e Geometria Analítica - Um curso de geometria analítica e álgebra linear, Reginaldo J. Santos- Ed: 1º - Capítulo 5.3 - Ex. 19

Mostre que o ângulo entre dois vetores não nulos e de , que é definido como sendo o número real entre e tal que:

está bem definido, ou seja, que existe um tal número real e é único. (Sugestão: mostre, usando a desigualdade de Cauchy-Schwarz., que )

Passo 1

Eaew, belezinha?

Vamos seguir pela sugestão dele, usando a desigualdade de Cauchy-Schwarz que diz que:

Vamos lembrar também uma propriedade de uma função modular neste contexto, saca só!

Passo 2

Obedecendo a desigualdade estabelecida por Cauchy-Schwarz, podemos dizer que:

Okay, temos então uma relação de desigualdade, e agora? Será que a definição dada é bem definida? Vamos checar!

Passo 3

Substituindo a função em nossa desigualdade temos:

Em temos que e , são os nossos pontos extremos da função cosseno, se observarmos o comportamento da função no intervalo temos o seguinte:

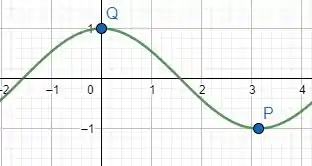
Note que em nenhum momento a desigualdade deixa de ter validade, portanto ela é sim, bem definida! A questão é isso, te vejo na próxima! Tchauzinho!

Resposta

Ao longo dos passos.

Exercícios de Livros Relacionados

Calcule o coseno do ângulo formado pelos vetores ( 1,4 , - 1 ) e ( 0,2 , 3 ) .

Dados u →=( 3,3 , 18 ) e v →=( 2 , - 2,1 ) , determine x → e y → tais que u→ = x → + y → , sendo x → paralelo a v → e y → ortogonal a v → .

Dados os vetores a →=( 1 , - 2 , - 1 ) e b →=( 0 , - 3,1 ) , determine um vetor u → , sabendo que u → é ortogonal a a → e b → , | u | →=315 e o ângulo formado por u → e o vetor ( 1,0 , 0 ) é agudo.

u →=( 2,1 , - 3 ) e v →=( 1,2 , 1 ) . Se w →=u→+λ v → , determine λ para que u→ e w → sejam ortogonais.Determine o coseno do ângulo que u→ forma com v → .

Sejam O A →=( 1,1 , 3 ) , O B →=( 3,2 , 2 ) e O C →=( 1,0 , - 4 ) .Ache as coordenadas de todos os vetores determinados pelos pontos O, A, B e C.Demonstre que os 4 pontos (não necessariamente na ordem