Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Álgebra Linear e Geometria Analítica - Reginaldo - Matrizes, Vetores e Geometria Analítica- Ed: 1º - Capítulo 7.3 - Ex. 11

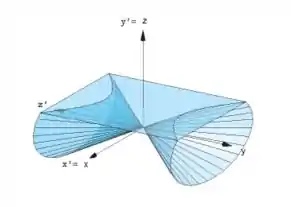
Mostre que a interseção de um cone circular com plano que não passa pelo seu vértice e uma cônica seguindo os seguintes passos:

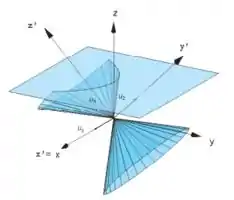
a) considere dois sistemas de coordenadas R = O , i → , j → , k →   e     S = O , i → , U 2 , U 3 , em que U 2 = ( 0 , cos ⁡ θ ,   sin ⁡ θ )     e     U 3 = ( 0 ,   - sin ⁡ θ ,   cos ⁡ θ ) , ou seja, o sistema S é obtido do sistema R por uma rotação do ângulo θ em torno do eixo x. mostre que é válida a seguinte relação entre as coordenadas, x ' , y ' , z ' , em relação ao sistema S e ( x , y , z ) , em relação ao sistema R

x ' y ' z ' = 1 0 0 0 cos ⁡ θ sin ⁡ θ 0 - sin ⁡ θ cos ⁡ θ     x y z = x ( cos ⁡ θ ) y + ( sin ⁡ θ ) z - ( sin ⁡ θ ) y + ( cos ⁡ θ ) z

b) mostre que o cone circular de equação

x ' 2 + y ' 2 = z ' 2

No sistema S tem equação

x 2 + ( cos ⁡ 2 θ ) y 2 + ( 2 sin ⁡ 2 θ ) y z - cos ⁡ 2 θ z 2 = 0

No sistema R.

c) Mostre que a interseção do cone com o plano z = 1 é cônica no plano de equação

x 2 + ( cos ⁡ 2 θ ) y 2 + ( 2 sin ⁡ 2 θ ) z = cos ⁡ 2 θ

d) Mostre que se θ = ± π 2 então a cônica é a parábola no plano de equação

x 2 ± 2 y = 0

e) mostre que se θ ≠ ± π 2 , então a cônica no plano tem equação

x 2 sec ⁡ 2 θ + y + tan ⁡ θ 2 sec 2 ⁡ 2 θ = 1 ,

Que é uma elipse se θ < π 4 e uma hipérbole se π 4 < θ ≤ π 2

Passo 1

Fala aí pessoal tudo blz?

Nessa questão pede para mostrar que a interseção de um cone circular com plano que não passa pelo seu vértice e uma cônica seguindo os seguintes passos:

a) considere dois sistemas de coordenadas R = O , i → , j → , k →   e     S = O , i → , U 2 , U 3 , em que U 2 = ( 0 , cos ⁡ θ ,   sin ⁡ θ )     e     U 3 = ( 0 ,   - sin ⁡ θ ,   cos ⁡ θ ) , ou seja, o sistema S é obtido do sistema R por uma rotação do ângulo θ em torno do eixo x. mostre que é válida a seguinte relação entre as coordenadas, x ' , y ' , z ' , em relação ao sistema S e ( x , y , z ) , em relação ao sistema R

x ' y ' z ' = 1 0 0 0 cos ⁡ θ sin ⁡ θ 0 - sin ⁡ θ cos ⁡ θ     x y z = x ( cos ⁡ θ ) y + ( sin ⁡ θ ) z - ( sin ⁡ θ ) y + ( cos ⁡ θ ) z

b) mostre que o cone circular de equação

x ' 2 + y ' 2 = z ' 2

No sistema S tem equação

x 2 + ( cos ⁡ 2 θ ) y 2 + ( 2 sin ⁡ 2 θ ) y z - cos ⁡ 2 θ z 2 = 0

No sistema R.

c) Mostre que a interseção do cone com o plano z = 1 é cônica no plano de equação

x 2 + ( cos ⁡ 2 θ ) y 2 + ( 2 sin ⁡ 2 θ ) z = cos ⁡ 2 θ

d) Mostre que se θ = ± π 2 então a cônica é a parábola no plano de equação

x 2 ± 2 y = 0

e) mostre que se θ ≠ ± π 2 , então a cônica no plano tem equação

x 2 sec ⁡ 2 θ + y + tan ⁡ θ 2 sec 2 ⁡ 2 θ = 1 ,

Que é uma elipse se θ < π 4 e uma hipérbole se π 4 < θ ≤ π 2

Só vem e confia que juntos vamos resolver esta questão

Passo 2

Na letra (a) sabendo que,

x ' y ' z ' = 1 0 0 0 cos ⁡ θ sin ⁡ θ 0 - sin ⁡ θ cos ⁡ θ     x y z = x ( cos ⁡ θ ) y + ( sin ⁡ θ ) z - ( sin ⁡ θ ) y + ( cos ⁡ θ ) z

Ficando,

R = O , i → , j → , k →   e     S = O , i → , U 2 , U 3

U 2 = ( 0 , cos ⁡ θ ,   sin ⁡ θ )     e     U 3 = ( 0 ,   - sin ⁡ θ ,   cos ⁡ θ )

R = O , cos 2 ⁡ θ , sin 2 ⁡ θ , 0   e     S = O , cos 2 ⁡ θ , U 2 , U 3

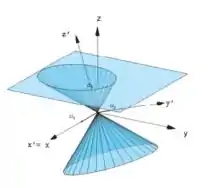
Na letra (b) sabendo que,

x ' 2 + y ' 2 = z ' 2

x 2 + ( cos ⁡ 2 θ ) y 2 + ( 2 sin ⁡ 2 θ ) y z - cos ⁡ 2 θ z 2 = 0

x = cos ⁡ θ  

y = sin ⁡ θ  

cos ⁡ θ 2 + ( cos ⁡ 2 θ ) ( sin ⁡ θ ) 2 + ( 2 sin ⁡ 2 θ ) ( sin ⁡ θ ) z - cos ⁡ 2 θ z 2 = 0

x ' 2 a 2 + y ' 2 b 2 = 1

Na letra ( c ) sabendo que,

x 2 + ( cos ⁡ 2 θ ) y 2 + ( 2 sin ⁡ 2 θ ) z = cos ⁡ 2 θ

z = 1

x 2 + y 2 = cos ⁡ 2 θ  

Na letra (d) sabendo que,

θ = ± π 2 x 2 ± 2 y = 0

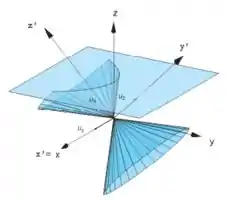
E por fina na letra (e) sabendo que,

x 2 sec ⁡ 2 θ + y + tan ⁡ θ 2 sec 2 ⁡ 2 θ = 1 , θ ≠ ± π 2

Que é uma elipse se θ < π 4 e uma hipérbole se π 4 < θ ≤ π 2

Espero ter ajudado, bons estudos e até a próxima.

Resposta

a)

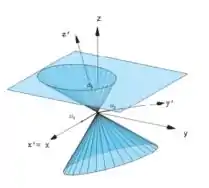
b) x ' 2 a 2 + y ' 2 b 2 = 1

c) x 2 + y 2 = cos ⁡ 2 θ  

d)

e)

Exercícios de Livros Relacionados

8. Identificar a superfície S e a sua interseção com o plano π dado. Representar graficamente esta interseção no plano π . b )S : 4 x 2 + 4 y 2 - z 2 = 0eπ : z = 4
6. Identificar e representar graficamente as superfícies expressas pelas equações nos intervalos dados. m )y 2 - x 2 = 16 ,0 ≤ z ≤ 4
6. Identificar e representar graficamente as superfícies expressas pelas equações nos intervalos dados. l )y 2 + 4 z 2 - 4 = 0 ,- 4 ≤ x ≤ 6
7. Identificar as superfícies definidas pelas equações, dizendo ao longo de que eixo elas ocorrem, conforme o caso. c )z = - 16 - x 2 - y 2
7. Identificar as superfícies definidas pelas equações, dizendo ao longo de que eixo elas ocorrem, conforme o caso. b )z = 9 - x 2 - y 2