Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Álgebra Linear e Geometria Analítica - Paulo Winterle - Vetores e Geometria Analítica- Ed: 2º - Capítulo 9.Problemas propostos - Ex. 7c

7. Identificar as superfícies definidas pelas equações, dizendo ao longo de que eixo elas ocorrem, conforme o caso.

c )   z = - 16 - x 2 - y 2

Passo 1

L e t r a   c :

Fala aí! Nesse exercício daqui estaremos trabalhando a seguinte equação:

z = - 16 - x 2 - y 2

POXA! Eu não sei se você está com as mesmas impressões que eu, mas se estiver, vai estar desconfiado de que esta equação nos representa uma esfera (ou pelo menos um pedaço dela). Vamos ver se é isso mesmo?

Passo 2

z = - 16 - x 2 - y 2

Elevando todo mundo ao quadrado...

z 2 = 16 - x 2 - y 2       →

x 2 + y 2 + z 2 = 16

AHA! Não falei contigo que essa equação era a equação de uma esfera (esfera de raio 4 )?

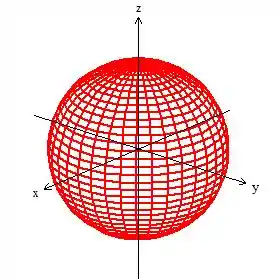
Passo 3

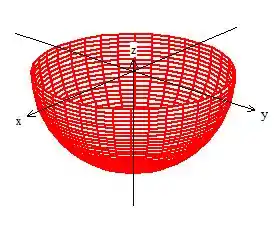
PORÉM... Calma jovem gafanhoto! Não é uma esfera inteira que queremos, já que temos aqui apenas parte negativa da raiz:

z = - 16 - x 2 - y 2

E sabemos que quando temos um quadrado (como z 2 ) e vamos isolar z , a gente tem que extrair mais ou menos a raiz:

z 2 = 16 - x 2 - y 2   →

z = ± 16 - x 2 - y 2

Viu só! E o que essas duas raízes representam? Bem, a positiva, representa a metade de cima da esfera enquanto que a parte negativa... A metade de baixo. Afinal, com as duas metades da laranja, se faz uma laranja inteira ;).

CONCLUSÃO: Como acabamos de falar, temos a metade de uma esfera de raio 4 , e essa metade é a de baixo já que a nossa raiz é negativa:

Resposta

Calota de esfera:

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Com as notações do exercício anterior, dado o ponto P'=( x',y ',0 ) em Π x y , obtenha as coordenadas do ponto P=( x ,y ,z ) no qual a semi-reta N P ′ intersecta a esfera unitária S2 .
Seja N=( 0 ,0 ,1 ) o polo norte da esfera unitária S 2={ ( x ,y ,z )∈R ³;x ²+y ²+z ² =1 } ³ ² ² ² . Para cada ponto P=( x ,y ,z ) diferente de N em S2 (isto é, c o mz ≠1 ), seja P'=( x',y ',0 ) o pont
Mostre que se a equação A x ²+B y ² +C z ²+D x y+E x z+F y z+G x+H y+I z+J=0 ² ² ² representa uma esfera então A=B=C≠ 0eD=E=F=0 . E reciprocamente, se estas condições são cumpridas, a equação dada rep
Completando os quadrados, identifique as superfícies de nível definidas por cada uma das formas quadráticas abaixo: 2 x 2 + y 2 - 4 x y - 4 y z
Completando os quadrados, identifique as superfícies de nível definidas por cada uma das formas quadráticas abaixo: 4 x 2 + y 2 - 8 z 2 + 4 x y - 4 x z + 8 y z