Enunciado
Álgebra Linear e Geometria Analítica - Paulo Winterle - Vetores e Geometria Analítica- Ed: 2º - Capítulo 9.Problemas propostos - Ex. 6m
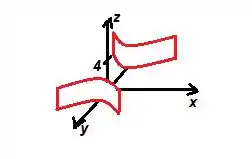
6. Identificar e representar graficamente as superfícies expressas pelas equações nos intervalos dados.
Passo 1
Fala aí! Nesse exercício daqui estaremos trabalhando a seguinte equação:
POXA! Essa equação no plano nos representa uma hipérbole ao redor do eixo :
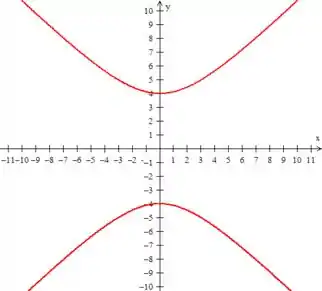
Então, a ausência do , indica que no , essa equação representará um CILÍNDRO ao redor do eixo , como vimos na teoria. Além disso, a sua diretriz é hiperbólica:
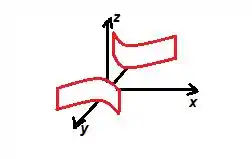
OBSERVAÇÃO: Esse é apenas um esboço da nossa superfície. Para terminar o desenho, precisamos de algumas informações extras!
Passo 2
- Repare que só queremos a parte que vai de até , já o exercício nos impôs a condição de que .
Com essas informações, e tendo em mente o nosso esboço do passo 1, podemos finalmente desenhar a nossa quádrica:
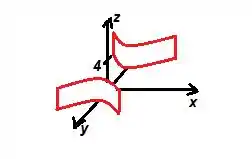
Viu só!
Resposta
Cilindro ao redor do eixo e de diretriz hiperbólica.
Exercícios de Livros Relacionados
Mostre que cada uma das equações representa uma superfície cônica com vértice na origem O = (0, 0, 0) e determine a equação de uma curva diretriz. d) x y + x z + y z = 0
Mostre que cada uma das equações representa uma superfície de revolução e determine o seu eixo de revolução e a equação de uma curva geratriz. c) y 6 - x 2 - z 2 = 0
Mostre que cada uma das equações representa uma superfície cônica com vértice na origem O = (0, 0, 0) e determine a equação de uma curva diretriz. c) 8 y 4 - y z 3 = 0
Mostre que a equação de uma superfície cônica com vértice num ponto P 0 = x 0 , y 0 , z 0 e uma curva diretriz situada no plano z = c com equação f x , y = 0 é f x 0 + c - z 0 z - z 0 x - x 0 , y 0 +
Mostre que cada uma das equações representa uma superfície de revolução e determine o seu eixo de revolução e a equação de uma curva geratriz. a) x 2 + y 2 - z 3 = 0