Enunciado
Álgebra Linear e Geometria Analítica - Paulo Boulos - Geometria Analítica - Ed: 3º - Capítulo 24.Exercício - Ex. 6
Obtenha uma equação da superfície esférica, conhecendo as extremidades de um diâmetro: e .
Passo 1
O segredo aqui é lembrar da definição de um diâmetro.
Um diâmetro é um segmento de reta que passa pelo centro da esfera e toca a superfície em dois pontos.
Vamos fazer um desenho para entender melhor:
Beleza, esse é um exemplo de um diâmetro.
Passo 2
O enunciado deu as coordenadas de dois pontos na superfície:
Pelo desenho da pra ver que o centro é o ponto médio entre e :
Ok, então ficamos assim:
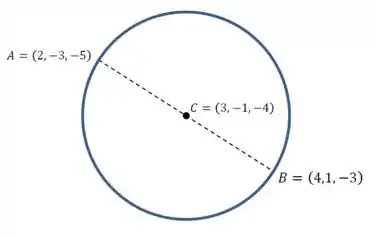
Passo 3
Como podemos calcular o raio da esfera? É só fazer a distância ou .
Então vamos fazer a distância :
Beleza, agora que já temos a posição do centro e o raio, é só lembrar da forma geral da equação da esfera.
Se a esfera tem raio e centro em , a equação é:
Então, no nosso caso:
Pronto! Essa é a equação que estávamos procurando.
Resposta
A equação da superfície esférica é .