Enunciado
Álgebra Linear e Geometria Analítica - Paulo Boulos - Geometria Analítica - Ed: 3º - Capítulo 24.Exercício - Ex. 8
Determine o diâmetro da superfície esférica que é perpendicular ao plano .
Passo 1
Bom pessoal, o primeiro passo é melhorar essa equação da esfera. Para isso vamos usar o método de completar quadrados:
Dá uma olhada nos termos com por exemplo:
Parecem muito com um produto notável que a gente conhece:
Então se somarmos dos dois lados:
Agora é só fazer a mesma coisa com os outros:
Então vamos somar dos dois lados:
Ok, agora fica mais fácil de trabalhar com a equação.
Passo 2
Se o diâmetro é perpendicular ao plano, então ele tem que ser paralelo ao vetor normal ao plano.
Quando temos uma equação geral de plano com essa forma aqui:
O vetor normal ao plano é:
Então, como o nosso plano é:
Então o nosso vetor normal é:
E para que um segmento qualquer seja paralelo a esse vetor, ele precisa atender:
E o comprimento desse vetor é:
Isso vai ser útil ali na frente!
Passo 3
Uma forma de resolver nosso problema agora é pegar o centro da esfera.
Lembrando que se a esfera tem raio e centro em , a equação é:
Então:
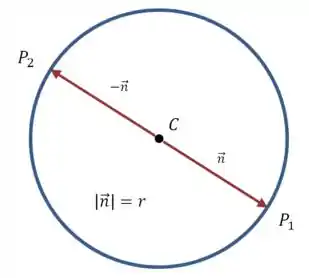
Ou seja, o nosso vetor tem comprimento igual ao raio!
Só o que a gente precisa fazer é andar um comprimento a partir do centro nos dois sentidos e vamos ter dois pontos na superfície que são ligados por um segmento paralelo a ·.
Passo 4
Então nosso primeiro ponto é:
E o segundo ponto é:
Ou seja, o nosso diâmetro é um segmento entre os pontos e .
Resposta
O diâmetro é um segmento entre os pontos e .