Enunciado
Álgebra Linear e Geometria Analítica - Paulo Boulos - Geometria Analítica - Ed: 3º - Capítulo 24.Exercício - Ex. 11
Sejam e as extremidades de um diâmetro da superfície esférica e um ponto distinto de e . Prove que:
(a) é uma equação de (equação diametral).
(b) pertence a se, e somente se, vê o diâmetro sob ângulo reto.
Passo 1
Então pessoal, se e são as extremidades do diâmetro, então o ponto médio entre eles é o centro da esfera :
E o raio da esfera é a metade do comprimento do segmento :
Lembrando que se uma esfera tem centro e raio , a equação é:
Então a equação da esfera é:
Beleza, vamos tentar seguir a partir daí.
Passo 2
Agora vamos lembrar desse produto notável:
Os termos para todas as variáveis são idênticos. Então para evitar confusão, vamos fazer para um termo só e então replicar o resultado para os outros.
Vamos usar os termos que dependem de :
Abrindo os dois produtos notáveis:
Cortando os termos iguais dos dois lados:
E somando dos dois lados:
Que é exatamente a forma da equação diametral, conforme o enunciado! Se você fizer exatamente a mesma coisa e somar tudo, vai chegar na igualdade que foi pedida.
Passo 3
O próximo passo é mostrar o que está nesse desenho aqui:
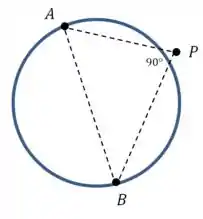
Isso quer dizer que os vetores e têm que ser ortogonais.
Se o ponto é:
Então:
Se os vetores são ortogonais, então o produto escalar é:
Resolvendo o produto escalar:
Que é exatamente a equação que nós encontramos lá em cima para um ponto na esfera ! Isso prova o que o enunciado pediu!
Todo ponto na esfera tem que enxergar o diâmetro sob um ângulo reto.
Resposta
(a) Demonstração.
(b) Demonstração.