Enunciado
Álgebra Linear e Geometria Analítica - Paulo Boulos - Geometria Analítica - Ed: 3º - Capítulo 24.Exercício - Ex. 9
Calcule a distância de à superfície esférica (isto é, a menor das distâncias de aos pontos de ).
Passo 1
Bom pessoal, o primeiro passo é melhorar essa equação da esfera. Para isso vamos usar o método de completar quadrados:
Dá uma olhada nos termos com por exemplo:
Parecem muito com um produto notável que a gente conhece:
Então se somarmos dos dois lados:
Agora é só fazer a mesma coisa com os outros:
Então vamos somar dos dois lados:
E para o :
Então vamos somar dos dois lados:
Ok, agora fica mais fácil de trabalhar com a equação.
Passo 2
A nossa ideia é encontrar a menor distância de até algum ponto na superfície da esfera.
Mas é muito complicado encontrar uma forma “geral” para os pontos na superfície da esfera! Então primeiro vamos encontrar a distância de até o centro da esfera.
Lembrando que se a esfera tem raio e centro em , a equação é:
Então no nosso caso:
E a distância de até o centro é:
Dá uma olhada nesse desenho para entender o que isso quer dizer:
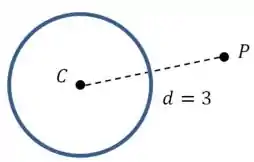
Passo 3
Mas o que o enunciado pediu foi a distância entre e a superfície da esfera.
Ou seja, queremos a distância entre e esse ponto vermelho no desenho:
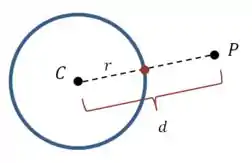
Pelo desenho dá pra ver que podemos calcular essa distância com essa conta aqui:
E o que quer dizer esse sinal negativo? Quer dizer que o nosso ponto estava, na verdade, no interior da esfera.
Mas isso não tem problema, é só considerar o módulo do valor calculado, então menor distância é:
Resposta
A distância de até a superfície esférica é .