Encontrar uma equação de hipérbole com focos nos vértices da elipse e vértices nos focos dessa elipse.

Da equação geral da elipse deitada temos:

Então comparando com a equação dada no enunciado temos:

Daqui tiramos que e . Vamos fazer um desenho dessa elipse:

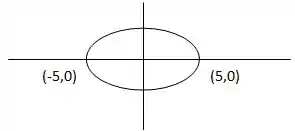
Os vértices dessa elipse são e . Esses vértices serão os focos da nossa hipérbole! Agora precisamos encontrar os focos da nossa elipse. A distância do centro até um dos focos de uma elipse vale . E a equação geral entre os parâmetros é:

E podemos achar o valor de :

Então os focos dessa elipse são e .

Tranquilo?

Agora vou desenhar em cima dessa elipse a nossa hipérbole. Ela deve ter focos nos vértices e vértices nos focos da elipse:

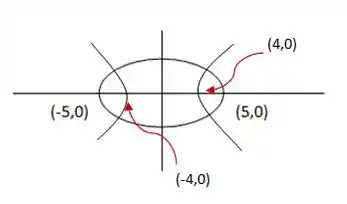
Indicado com as setas em vermelho estão os pontos dos vértices da nossa hipérbole. Na hipérbole a distância entre o centro e um dos focos é e nesse caso temos que . E temos que a distância entre o centro e o vértice é o parâmetro , que nesse caso vale .

Na hipérbole a relação fundamental é um pouco diferente e é dada por:

Assim para achar o parâmetro é só substituir os valores e resolver pra :

Beleza até aqui?

Resumindo os parâmetros da nossa hipérbole:

E como a elipse era deitada, a nossa hipérbole também é deitada! Daí resgatando do livro texto a equação da hipérbole deitada temos:

Agora é só substituir os parâmetros:

E para deixar na forma mais geral, precisamos fazer algumas continhas. Começando pelo :

Agora sim! A equação da hipérbole é .

Espero ter ajudado!

Vamos pra próxima?