Enunciado
Álgebra Linear e Geometria Analítica - Paulo Boulos - Geometria Analítica - Ed: 3º - Capítulo 12.Exercício - Ex. 5
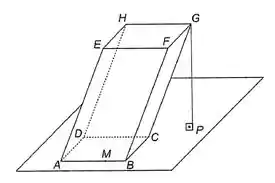
No paralelepípedo representado na figura, a área da base é e a aresta tem comprimento . O ângulo mede ( é perpendicular ao plano ) e o ponto é tal que . Calcule , sabendo que está orientado por uma base sinistra.
Passo 1
Antes de tudo vamos lembrar: uma base sinistra não quer dizer que ela é irada hahaha quer dizer que ao invés de obedecer a regra da mão direita, ela obedece a regra da mão esquerda?
Sabemos que:
Onde é o ângulo que forma com .
Porém, sabemos que , então:
Passo 2
Vamos pensar uma coisa: como são vetores diretores do plano da base, o produto vetorial deles é um vetor normal do plano não é? Então é paralelo a .
Então, o ângulo que queremos é o ângulo
é a área do paralelogramo da base, ou seja, .
E , de acordo com o enunciado, vale :
Então: