Enunciado
Álgebra Linear e Geometria Analítica - Paulo Boulos - Geometria Analítica - Ed: 3º - Capítulo 11.Exercício - Ex. 30
No paralelepípedo retângulo mostrado na Figura 11-9, é o centro da face , e e são, respectivamente, os pontos médios das arestas e . Mostre que é perpendicular ao plano se, e somente se, a face é uma quadrado de diagonal congruente à aresta .
Passo 1
Nesse tipo de problema a primeira coisa que você deve fazer é definir uma base:
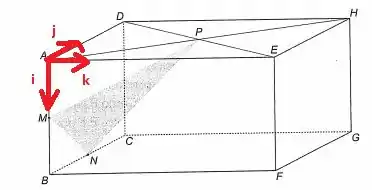
Escolhi a base , ortonormal e positiva, com os vetores mostrados na figura. Vamos supor que o lado mede , mede e mede . Assim,
Para que seja perpendicular ao plano , devemos ter que
Isso deve ocorrer por o produto vetorial é perpendicular ao plano e, para que também seja, eles devem ser paralelos! Assim, o primeiro passo é escrever as coordenadas de cada um desses vetores na base escolhida!
Passo 2
Note que
Mas sabemos que
Assim,
Agora vamos olhar para :
Assim,
Analogamente,
Mas
Assim,
Já o vetor :
Passo 3
Fazendo o produto vetorial:
Como só estamos interessados na direção do vetor, vamos esquecer o , de modo que a equação que temos que resolver é
Assim,
Para demonstrar o que a questão pediu, temos que obter duas coisas:
Isolando na primeira equação:
Substituindo na segunda:
Fazendo o mesmo na terceira:
Como , e por hipótese, temos que
Assim, provamos o que o exercício pedia: a face é uma quadrado () e sua diagonal é congruente à aresta ()!
Resposta
Demonstração.