Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Álgebra Linear e Geometria Analítica - Paulo Winterle - Vetores e Geometria Analítica- Ed: 2º - Capítulo 3.Problemas propostos - Ex. 1c

Se vec u = 3 vec i - vec j - 2 vec k , vec v = 2 vec i + 4 vec j - vec k e vec w = - vec i + vec k , determinar:

c) (vec u xx vec w) + ( vec w xx vec u )

Passo 1

Vou começar te falando de uma propriedade do produto vetorial, que é mata essa questão rapidinho, é a seguinte:Para qualquer vec u e vec w , podemos afirmar que vec u xx vec w = - vec w xx vec u

Maaas como acontece esquecer essas propriedades, vamos fazer o passo a passo para encontrar esse módulo!

Passo 2

Para achar o produto vetorial entre dois vetores vamos achar o determinante da seguinte matriz:

vec a xx vec b = |[[i,j,k],[x_a,y_a,z_a],[x_b,y_b,z_b]]|

Para achar esse determinante, temos o método de Sarraus, que fica assim:

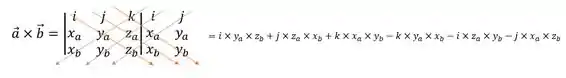
Credo né?? Relaxa que com os números fica mais bonitinho!! 😊

Como temos que nosso produto é vec u xx vec w e vec u = ( 3 , - 1 , - 2 ) e vec w = ( - 1,0 , 1 ) , ficamos com

vec u xx vec w = |[[i,j,k],[3,-,1,-,2],[-,1,0,1]]|

Passo 3

Para fazer esse determinante vamos resolver o determinante, vamos fazer a regra de Sarrus (a que foi mostrada no passo 2) ficamos com:

i xx (- 1) xx 1 + j xx (- 2) xx (- 1) + k xx 3 xx 0 - k xx (- 1) xx ( - 1 ) - i xx (- 2) xx 0 - j xx 3 xx 1

Simplificando isso dai, ficamos com:

vec u xx vec w = - i + 2 j - k - 3 j

vec u xx vec w = - i - j - k

Passo 4

Agora para vec w xx vec u , ficamos com

vec w xx vec u = |[[i,j,k],[-,1,0,1],[3,-,1,-,2]]|

E seu determinante é:

i xx 0 xx (- 2) + j xx 1 xx 3 + k xx (- 1) xx (- 1) - k xx 0 xx 3 - i xx 1 xx (- 1) - j xx (- 1) xx ( - 2 )

vec w xx vec u = 3 j + k + i + 2 j

vec w xx vec u = i + j + k

Passo 5

Então ficamos com

(vec u xx vec w) + (vec w xx vec u) = (- i - j - k) + ( i + j + k )

(vec u xx vec w) + (vec w xx vec u) = vec 0

Resposta

(vec u xx vec w) + (vec w xx vec u) = vec 0

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Se u → = 3 i → - j → - 2 k → , v → = 2 i → + 4 j → - k → e w → = - i → + k → , determinar:e) u → - v → × w →
Se vec u = 3 vec i - vec j - 2 vec k , vec v = 2 vec i + 4 vec j - vec k e vec w = - vec i + vec k , determinar:| vec u xx vec u |
Se vec u = 3 vec i - vec j - 2 vec k , vec v = 2 vec i + 4 vec j - vec k e vec w = - vec i + vec k , determinar:f) (vec u xx vec v) xx vec w
Se vec u = 3 vec i - vec j - 2 vec k , vec v = 2 vec i + 4 vec j - vec k e vec w = - vec i + vec k , determinar:b)( 2 vec v ) xx ( 3 vec v )
Se u → = 3 i → - j → - 2 k → , v → = 2 i → + 4 j → - k → e w → = - i → + k → , determinar:d) ( u → × v → ) × ( v → × u → )