Uma pequena fábrica produz copos comuns e copos de vinho. Uma máquina automatiza parte do processo de fabricação. Para produzir uma caixa de copos comuns requer-se 1 hora de uso da máquina mais 1 hora de trabalho de um operário. A produção de uma caixa de copos de vinho requer apenas meia hora de uso da máquina, mas ocupa 2 horas de trabalho operário. No período de uma semana, a fábrica dispõe de 80 horas de trabalho manual e 50 horas de uso da máquina. O lucro na venda de uma caixa de copos de vinho é de 50 reais e, numa caixa de copos comuns, o lucro é de 40 reais.
a) Qual deve ser a produção semanal de cada tipo de copo de modo a maximizar o lucro?
Passo 1
Salve galera estudiosa, tudo certin?? É hora da resolução!!! Vamos lá??
Vamos definir as seguintes variáveis para o nosso problema:
X: número de caixas de copos comuns produzidas
Y: número de caixas de copos de vinho produzidas
Analisando o contexto do problema temos as seguintes desigualdades:
Além disso, é óbvio que a produção de copos comuns e de vinho precisa ser maior ou igual a zero, logo:
Representando cada uma dessas desigualdades no plano cartesiano, temos a seguinte região:
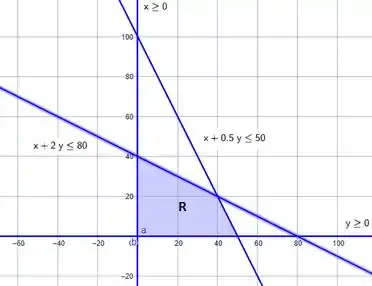
Passo 2
Desejamos agora encontrar nessa região os valores para X e Y que maximizem o nosso lucro, que é dado pela função:
Um método prático de achar o ponto de máximo da função L consiste em calcular L(P) para todo vértice P da nossa região R e ver qual desses valores é o maior.
Observando melhor a região, conseguimos determinar os vértices A, B e C como potenciais candidatos à maximizar o lucro.
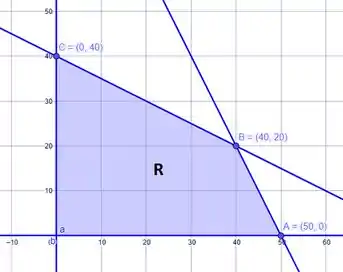
Calculando os Lucros, temos:
Logo, percebemos que a melhor solução é o ponto B, ou seja, para maximizar o lucro a fábrica precisa produzir 40 caixas de copo comum e 20 caixas de copo de vinho por semana.
Resposta
- 40 caixas de copo comum e 20 caixas de copo de vinho.