Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Álgebra Linear e Geometria Analítica - Paulo Boulos - Geometria Analítica - Ed: 3º - Capítulo 12.Exercício - Ex. 14a

A pirâmide mostrada na Figura 12-6 (b) tem por base um quadrado de lado 2. As arestas que contêm o vértice V formam ângulos de 45 ° com o plano do quadrado, e a base V A → ,   V D → ,   V B → é postiva.

(a) Calcule D C → ,   D A → / 2 ,   D V → .

Passo 1

Bora lá!

Para esse exercício nós iremos usar um sistema de coordenadas x , y , z ortogonal positivo, tendo origem no ponto O . O eixo x é paralelo à aresta A B → com sentido para direita, o eixo y é paralelo à aresta A D → e o eixo z é paralelo à altura do tetraedro.

Passo 2

Para calcularmos a atura do nosso tetraedro, tem que o ângulo A O ^ V = 90 ° e O A ^ V = 45 ° .

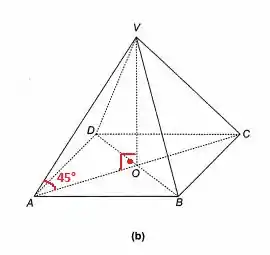
Portanto:

t g 45 ° = 1

O A - O V - = 1 ⇒ O V - = O A - = l 2 2 = 2 2 2 = 2

Passo 3

Agora, vamos escrever todos os vértices do tetraedro em relação ao sistema de coordenadas adotado:

O = 0 ,   0 ,   0

A = - 1 ,   - 1 ,   0

B = ( 1 ,   - 1 ,   0 )

C = ( 1 ,   1 ,   0 )

D = ( - 1 ,   1 ,   0 )

V = ( 0 ,   0 ,   2 )

Passo 4

Queremos calcular o produto misto D C → , D A → 2 ,   D V → . Então, os vetores em questão são:

D C → = C - D = 1 ,   1 ,   0 - - 1 ,   1 ,   0 = 2 ,   0 ,   0

D A → 2 = A - D 2 = - 1 ,   - 1 ,   0 - - 1 ,   1 ,   0 2 = ( 0 ,   - 1 ,   0 )

D V → = V - D = 0 ,   0 ,   2 - - 1 ,   1 ,   0 = 1 ,   - 1 ,   2

Passo 5

Por fim, como esses valores estão escritos em relação a uma base ortonormal positiva, basta calcularmos o determinante, temos então:

D C → , D A → 2 ,   D V → = 2 0 0 0 - 1 0 1 - 1 2 = - 2 2

Resposta

(a) D C → , D A → 2 ,   D V → = - 2 2 .

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Dados O A →=( 2 , - 1,0 ) , O B →=( 1 , - 2,1 ) e O C →=( 1,0 , 2 ) , determine um vetor O D →=( x , y , z ) tal que O D → ,O A → ∧ O B → , O A → ∧ O C → sejam l.d., O D → ⋅ O B → = - 28 e o volume do
Sejam A B →=( 3,6 , 3 ) , A C →=( 1,3 , - 2 ) e A D →= ( 2,2 , α - 2 ) . Encontre os valores do parâmetro α para os quais o volume V do tetraedro A B C D fica igual a 3 .
No tetraedro A B C D , temos A B →=( 7,7 , - 7 ) , A C →=( 9,5 , - 10 ) e A D →= ( 11,7 , - 1 ) . Calcule a altura do tetraedro relativa ao vértice A .
No tetraedro O A B C , temos: O A →= a → , O B →= b → e O C →= c → , M é o ponto médio de A C → , N é o ponto médio de A B → e P é o ponto médio de B C → . Qual é a relação entre o número [ O M , → O
Mostre que U ⋅ V × W = V ⋅ W × U = W ⋅ ( U × V ) . (Sugestão: use as propriedades do determinante)