Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Álgebra Linear e Geometria Analítica - Vetores e uma iniciacao a geometria analitica mello e watanabe- Ed: 2º - Capítulo 1.Exercícios Propostos - Ex. 13

No triângulo ABC, C A → = a → e C B → = b → ; X é tal que X B → = 3 A X → e Y é tal que 3 Y C → = 2 Y B → .

  1. Coloque X e Y na figura, em posição correta, fazendo os cálculos necessários.
  2. Escreva C X → , A Y → e X Y → em função de a → e b → .

Passo 1

  1. Galera, o segredo para resolver essa questão é o seguinte: X B → = 3 A X → , então esses dois vetores são paralelos, mas não tem a mesma origem. Isso é muito importante porque quer dizer que X está posicionado na linha entre A e B . Já no caso de Y, temos 3 Y C → = 2 Y B → , o que indica que Y está posicionado na linha entre C e B mas fora do triângulo. Então começamos desenhando um triângulo genérico:

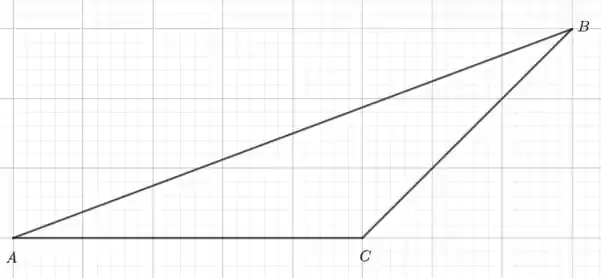
    2. Depois, nós devemos notar que

    A B → = A X → + X B → = A X → + 3 A X → = 4 A X → ⇒ A X → = 1 4 A B →

    Y B → = Y C → + C B → ⇒ C B → = Y B → - Y C → = 3 2 Y C → - Y C → = 1 2 Y C → ⇒ Y C → = 2 C B → = 2 b → ⇒ Y B → = 3 2 Y C → = 3 b →

    Agora, sabemos que X está posicionado a 1 4 do caminho de A a B e Y está posicionado a de modo que o tamanho de Y C → seja o dobro de b → , como desenhado abaixo:

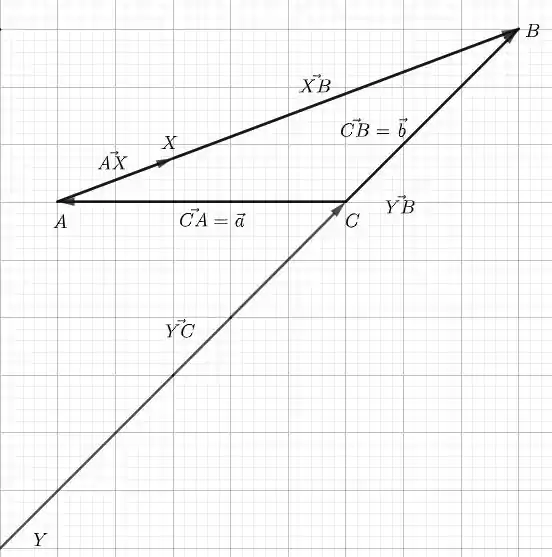
    Passo 2

  2. Agora temos que escrever C X → , A Y → e X Y → em função de a → e b → . Para facilitar a visualização, vamos desenhar cada um desses vetores na figura abaixo.

A partir da figura, podemos ver que

C X → = C A → + A X → = a → + 1 4 A B → = a → + 1 4 ( - a → + b → ) = 3 4 a → + 1 4 b →

onde usamos o fato de que A B → = A C → + C B → = - C A → + C B → = - a → + b → .

No caso de A Y → é um pouco mais fácil, uma vez que podemos ir de A a Y também pelo caminho ACY. Veja só:

A Y → = A C → + C Y → = - C A → - Y C → = - a → - 2 b →

onde usamos o fato de que Y C → = 2 b → que foi obtido lá no Passo 1.

Por último, mas não menos importante, vamos obter X Y → . Na figura, vemos que podemos ir de X a Y tanto pelo caminho XCY, por exemplo. Assim, temos

X Y → = X C → + C Y → = - C X → - Y C → = - 3 4 a → - 1 4 b → - 2 b → = - 3 4 a → - ( 1 + 8 4 ) b →

X Y → = - 3 4 a → - 9 4 b →

onde usamos os resultados C X → = 3 4 a → + 1 4 b → e Y C → = 2 b → .

Resposta

C X → = 3 4 a → + 1 4 b →

A Y → = - a → - 2 b →

X Y → = - 3 4 a → - 9 4 b →

Exercícios de Livros Relacionados

Verifique se o vetor U é combinação linear (soma de múltiplos escalares) de V e W : (a) V = 5 , 4 , - 3 , W = ( 2 , 1 , 1 ) e U = ( - 3 , - 4 , 1 )
Verifique se o vetor U é combinação linear (soma de múltiplos escalares) de V e W : (a) V = 9 , - 12 , - 6 , W = ( - 1,7 , 1 ) e U = ( - 4 , - 6,2 )
Considere dois vetores V e W tais que V = 5 e W = 2 e o ângulo entre V e W é 60 ° . Determine como combinação linear de V e W x V + y W : (a):Um vetor X tal que X . V = 20 e X . W = 5 .
Verifique que o polinômio t 2 + 2 t + 7 é combinação linear (soma dos múltiplos escalares) de t 2 + 1 e t + 3 .
Verifique que a função constante a 3 é combinação linear de g t = 5 t a n 2 t e h t = 2 c o s 2 ( t ) .