Enunciado
Álgebra Linear e Geometria Analítica - Paulo Boulos - Geometria Analítica - Ed: 3º - Capítulo 1.Exercício - Ex. 5
- Prove que:
Passo 1
Mais uma vez estamos lidando com vetores, então vamos desenhar os vetores genéricos para fazer essas questões.
Passo 2
Vamos lá então desenhar esses segmentos orientados, com valores genéricos!
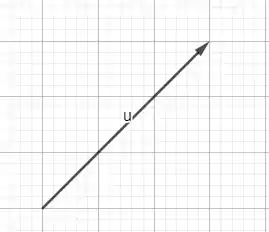
Desenhamos o vetor , faremos agora o vetor .
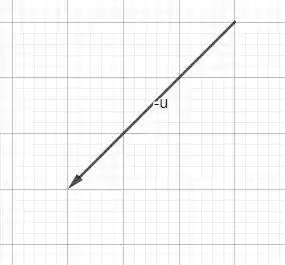
Agora vamos fazer o , que é o inverso do vetor acima, vai dar isso aqui:
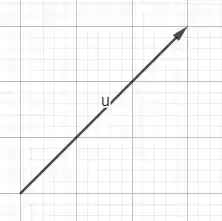
O próprio vetor é o inverso do que desenhamos.
Passo 3
Agora vamos para a segunda demonstração. Nessa não desenharemos apenas usaremos conceitos!
Um vetor oposto tem sempre o sentido contrário do vetor original.
Então quando um vetor oposto a outro serão iguais???
Ora, se os vetores são iguais. Eles precisam ter MESMO SENTIDO!! Só que vetores opostos tem sentidos contrários! Para isso ocorrer, o vetor vai ter que ser um ponto, pois pontos não tem sentido! E o ponto é o vetor nulo.
Então se , podemos afirmar que .
Resposta
Ei, a resposta está no passo a passo :)