Enunciado
Álgebra Linear e Geometria Analítica - Cálculo Volume 2 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 12.1 - Ex. 43
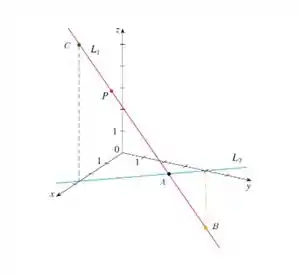
A figura mostra uma reta no espaço e uma segunda reta , que é a projeção de no plano . (Isto é, os pontos de estão diretamente abaixo ou acima do pontos de
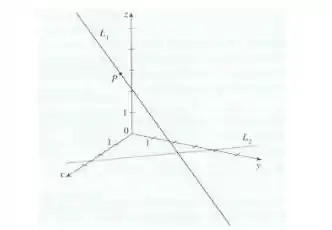
- Determine as coordenadas do ponto da reta .
- Localize no diagrama os pontos e onde a reta , intercepta os planos e , respectivamente.
Passo 1
- Vamos desenhar uma linha vertical do ponto até a reta (e, portanto, o plano ). Ao desenhar a reta até este ponto de projeção paralelo aos eixos e , descobrimos que o ponto de projeção é . Então só falta descobrir a coordenada do ponto .
- Como é a projeção de no plano e passa pelo plano , a interseção de com o plano será a interseção de e , que chamaremos de ponto .
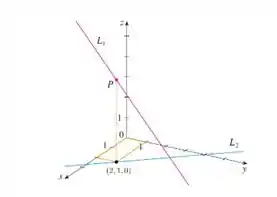
Para encontrar essa coordenada, podemos completar o retângulo, desenhando linhas paralelas, assim:
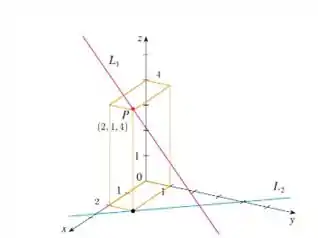
Dessa forma, podemos perceber que a coordenada do ponto é . Então nosso ponto será .
Passo 2
A interseção de com o plano estará abaixo da intersecção do eixo com Assim, desenhamos uma reta vertical abaixo deste ponto, e a interseção dela com será , como mostrado.
A interseção de com o plano estará acima da intersecção do eixo de no plano . Então, como antes, podemos desenhar uma reta vertical a partir deste ponto, e a interseção desta reta com será
Resposta
Exercícios de Livros Relacionados
Determinar o valor de n para que o vetor v → = n , 2 5 , 4 5 seja unitário.
Verificar se são unitários os seguintes vetores: u → = 1,1 , 1e v → = 1 6 ,- 2 6 , 1 6
Seja o vetor v → = m + 7 i → + m + 2 j → + 5 k → . Calcular m para que v → = 38 .
A B C D é um trapézio, A B → = a → ,D C → = 2 a → e D A → = b → . O ponto E é tal que B E → = 1 3 B C → . Escreva A C → e D E → em função de a → e b → .
São dados O A → = a → , O B → = b → ,O C → = c → ,A P → = 1 3 c → ,B Q → = 4 5 a → . Escreva P Q → em função de a → ,b → e c → .