Exercícios de Introdução aos Vetores - Lista de Exercícios Resolvida

Calcule o módulo do vetor = (2, 6, 3).

Sabendo que a distância entre os pontos e é , calcular .

Determinar os valores de e para que sejam paralelos os vetores e .

Dados os pontos e , determinar as coordenadas de um ponto tal que os vetores e sejam paralelos.

Dado que = (2, y, 1) e , calcule y.

Determinar a extremidade do segmento que representa o vetor , sabendo que sua origem é o ponto .

Obter um ponto do eixo das abscissas equidistantes dos pontos e .

Considere um sistema de coordenadas xado em e as retas e dadas pelas equações

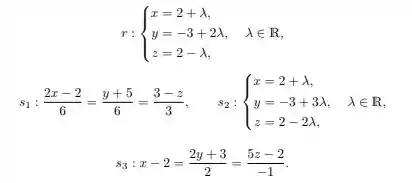
(a)

(b)

(c)

(d)

(e)

Considere fixado um sistema de coordenadas , em que é uma base ortonormal de e sejam os pontos dados por

Seja a reta que passa pelo ponto e é ortogonal tanto à reta que passa pelos pontos como à reta que passa pelos pontos . Assinale a alternativa correspondente a uma equação para r:

(a)

(b)

(c)

(d)

(e)

Sejam dados vetores distintos em e sejaw}. Considere as seguintes afirmações:

(I) se , então é linearmente dependente;

(II) se é ortogonal a e a , então é linearmente independente;

(III) se é linearmente dependente, então existem tais que é igual

a .

Está correto o que se afirma em:

1. Somente em 1
2. 1 e 3 apenas
3. 1,2 e 3
4. 1 e 2 apenas
5. 2 e 3 apenas

Seja uma base de e considere os vetores

Se são tais que , então é igual.

Sejam pontos que não pertençam a uma mesma reta e considere o vetor

Seja o ponto tal que o vetor seja paralelo a e tal que seja paralelo

a . Assinale a alternativa correta:

Sejam dados vetores tais que e a medida do ângulo entre seja igual a . Dado , temos que

se e somente se, é igual a:

Seja uma base ortonormal de e considere os vetores . Suponha que seja uma base ortogonal de tal que tem a mesma direção que , e tal que é uma combinação linear de .

Se são tais que , então:

Considere os vetores e

(e) Determine a equação geral da reta que contém o ponto e vetor diretor .

Considere os vetores e

(b) e são ortogonais (perpendiculares)? Justifique.

Considere os vetores e

(d) Determine a projeção de em .

Considere os vetores e

(c) Determine um vetor de mesma direção que e comprimento igual a .

Considere os vetores e

(a) Determine o comprimento do vetor .

Considere , e .

b) Determine o vetor .

Escreva como combinação linear dos vetores , e . Mostre que o conjunto gerado por , , , é igual ao conjunto gerado por , , .

Q15. Seja fixado um sistema de coordenadas no espaço, com uma base ortonormal, e considere o elipsóide de equação:

Assinale a alternativa contendo três vetores que sejam paralelos aos eixos de simetria desse elipsoide:

3. ;
4. ;
5. ;

Considere a reta r de equação

E seja o ponto simétrico ao ponto em relação a r, isto é, o ponto tal que seja ortogonal a r e o ponto médio do segmento PQ esteja em r. Temos que é igual a:

Considere as seguintes afirmações

Então está certo o que se afirma em

Considere as seguintes afirmações sobre os vetores em

Assinale a alternativa correta

Sejam vetores tais que e tais que a medida

do ângulo entre seja igual a . Temos que o cosseno do ângulo entre

é igual a:

Considere em um tetraedro regular de aresta unitária e seja o ponto da semirreta de origem passando por tal que

em que denota a distância entre os pontos . Temos que o produto

escalar dos vetores e é igual a:

Seja um polinômio de grau que passa pelos pontos. Então vale:

(A)

(B)

(C)

(D)

Sejam uma base ortonormal de e , vetores não nulos tais que

é paralelo a e é ortogonal a . Temos que é igual a:

(a)

(b)

(c)

(d)

(e)

Considere fixada uma orientação em . Sejam , vetores tais que o produto misto seja igual a . Temos que

é igual a:

(a)

(b)

(c)

(d)

(e)

Seja uma base ortonormal de e considere um triângulo em tal que:

Temos que o comprimento da altura desse triângulo relativa à base é igual a:

(a)

(b)

(c)

(d)

(e)

Considere fixada uma orientação em . Sejam e tais que

Se o ângulo entre e é obtuso, então é igual a:

(a)

(b)

(c)

(d)

(e)

Sejam , bases de e a matriz cujas colunas são , e . Se

E se é tal que e para certos , então é igual a:

(a)

(b)

(c)

(d)

(e)

Considere fixada uma orientação em . Sejam e , e considere o vetor dado por

Se , , e a medida do ângulo entre e é igual a , então pode-se afirmar que:

(a) ou

(b) ou

(c) ou

(d) ou

(e) ou

Considere fixada uma orientação em . Seja um tetraedro em tal que:

E tal que a medida do ângulo entre os vetores e é igual a . Se a medida do ângulo entre os vetores e for igual a , então o volume desse tetraedro será igual a:

(a)

(b)

(c)

(d)

(e)

Considere fixado um sistema de coordenadas em . Sejam e e as retas dadas pelas equações:

Se e são concorrentes, então é igual a:

(a)

(b)

(c)

(d)

(e)

Sejam e tais que , e . Suponha que a medida do ângulo entre e seja igual a e que a medida do ângulo entre e seja igual a . Temos que a projeção ortogonal de sobre é igual a:

(a)

(b)

(c)

(d)

(e)

Seja uma base ortonormal de e considere os vetores:

Se e é um triângulo em tal que e , então a área desse triângulo é igual a:

(a)

(b)

(c)

(d)

(e)

Considere fixada uma orientação em . Sejam e com . Assinale a alternativa correta:

(a) se , então é ortogonal a

(b) se é ortogonal a , então

(c) o produto misto é nulo se, e somente se, é combinação linear de e

(d) se é linearmente dependente, então é paralelo a

(e)

Considere fixado um sistema de coordenadas , em que é uma base ortonormal de . Sabe-se que as retas

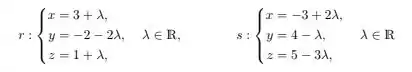
são concorrentes. Seja a reta ortogonal a e a que passa pelo ponto de interseção entre . Assinale a alternativa correspondente a um ponto que pertence a :

(a)

(b)

(c)

(d)

(e)

Considere fixado um sistema de coordenadas em . Sejam as retas

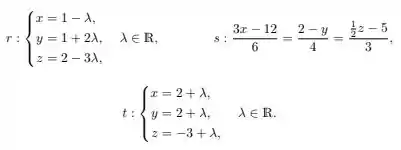
Assinale a alternativa correta:

(a) são paralelas distintas e são reversas

(b) são paralelas distintas e são concorrentes

(c) e são reversas

(d) são reversas e são concorrentes

(e) são reversas e são reversas

Um sistema em variáveis:

(A) com equações tem infinitas soluções.

(B) homogêneo com equações pode ter infinitas soluções.

(C) com equações tem solução única.

(D) com equações não tem solução.